Question

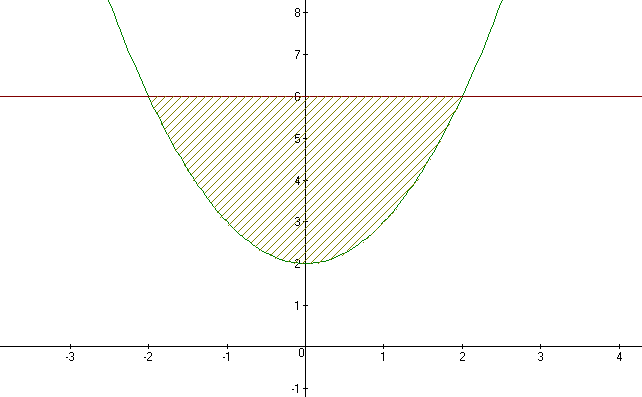
вычислить площадь фигуры ограниченной линиями y=x^2+2 ;Y=6

Answer 1

Точки пересечения графиков y=x^2+2  ;Y=6
х_1 = - 2 и х_2 = 2, таким образом пределы интегрирования от -2 до +2
Площадь фигуры ограниченная кривыми равна определенному интегралу
$S = intlimits^2_{-2} 6 ,dx - intlimits^2_{-2} {x^2} , dx = 6x|_{-2}^2 - frac{x^3}{3}|_{-2}^2 = 10 frac{2}{3}$  кв. ед.