Question

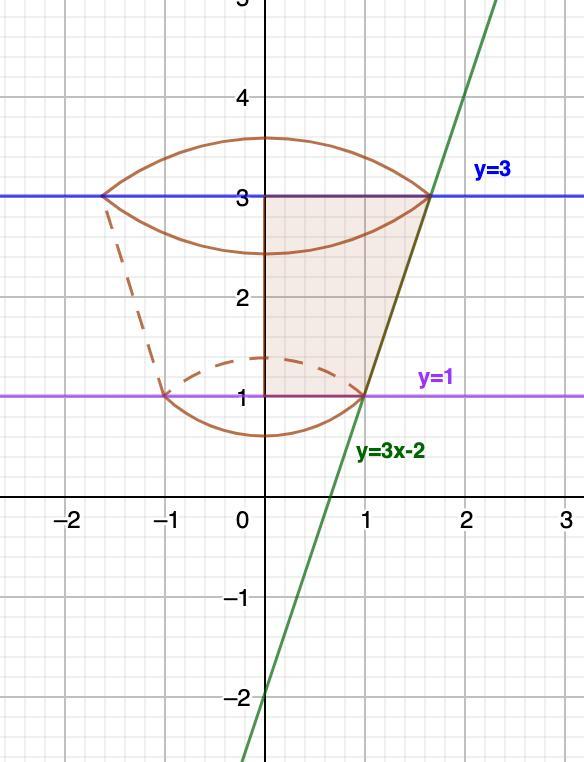
вычислите объем тела, образованного при вращении вокруг оси Оу фигуры, ограниченной линиями: у=3х-2, х=0, у=1, у=3​

Answer 1

Ответ:

Объяснение:

у=3х-2, х=0, у=1, у=3​.

Построим данные графики и изобразим тело вращения. (см. рис.)

Объем тела, образованного при вращении вокруг оси Оу, находится  по формуле:

$\displaystyle V_y=\pi \int\limits^{y_2}_{y_1} {x^2} \, dy$

Выразим х:

$\displaystyle y=3x-2\;\Rightarrow \;x=\frac{y+2}{3}$

Найдем объем:

$\displaystyle V_y=\pi \int\limits^3_1 {\frac{(y+2)^2}{9} } \, dy=\frac{\pi }{9}\int\limits^3_1 {(y^2+4y+4)} \, dy=\frac{\pi }{9}\left(\frac{y^3}{3} +4*\frac{y^2}{2}+4y\right)\;|^3_1 =\frac{\pi }{9}\left(\frac{27}{3 }+2*9+4*3- \frac{1}{3}-2-4\right)=3\frac{17}{27}\pi \;(ed^3)$