Предмет: Алгебра,
автор: andrewmerzlikin7
Помогите ПОЖАЛУЙСТА!!!
НУЖНО ДОКАЗАТЬ ТОЖДЕСТВО
Приложения:
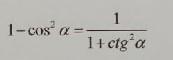
Ответы
Автор ответа:
1
Ответ:
Объяснение:
доказать тождество
воспользуемся формулами
1) преобразуем левую часть
2) преобразуем правую часть
3) левая часть равна правой sin²α = sin²α
тождество доказано
Похожие вопросы
Предмет: Алгебра,
автор: Gxdhvcdgcbbv
Предмет: Математика,
автор: Дарья1011111
Предмет: Алгебра,
автор: jeckson2003
Предмет: Геометрия,
автор: katytixomirova
Предмет: Английский язык,
автор: Aztzky