Предмет: Алгебра,
автор: anzhelikakarlos
Помогите , пожалуйста, с алгеброй
Приложения:
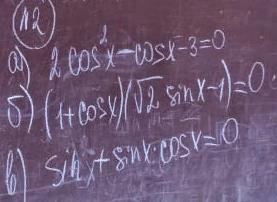
Ответы
Автор ответа:
1
Объяснение:
a) Произведем замену: cosx=t, получаем следующее:
x=1,5 нам не подходит, т.к. -1<=cosx<=1
Где n - целое число
б) Тут либо первая скобка равна нулю, либо вторая равно нулю:
где n-целое число
где n - целое число.
в)
либо правая часть равна нулю:
где n-целое число.
Либо левая часть равна нулю:
где n-целое число.
darakolasni:
Если помог, отметьте как лучший ответ)
Похожие вопросы
Предмет: Алгебра,
автор: Аноним
Предмет: Биология,
автор: Nastya7111
Предмет: Информатика,
автор: Mashi201199
Предмет: Геометрия,
автор: DiAnNa123er
Предмет: Математика,
автор: Vys