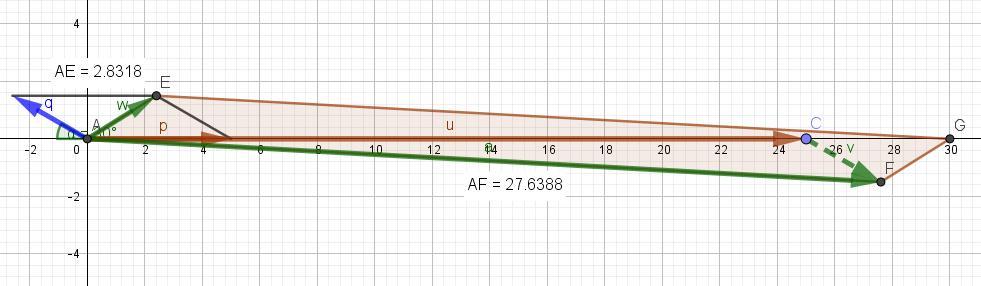
Вычислить площадь параллелограмма построенного на векторах a и b
a=5p-q b = p+q |p|=5 |q|=3 (p^q)=5П/6
Ответы
Эта задача может быть решена в двух вариантах:
1) по длинам векторов a и b и углу между ними,
2) по координатам векторов и их векторному произведению.
1) Длину векторов а и b и угол наклона их к оси Ох определяем по теореме косинусов:
a = √((5*5)² + (-3)² - 2*25*3*cos(5π/6)) = √(625 + 9 - 150*(-√3/2)) =
= √(634 + 75√3) ≈ √763,9038 ≈ 27,6388.
cosβ = (25² + (634 + 75√3) - 9)/(2*25*√(634 + 75√3)) ≈ 0,998526.
Угол β = 3,111057 градуса.
b = √(5² + 3² - 2*5*3*cos(π-(5π/6))) = √(25 + 9 - 30*(√3/2)) =
= √(34 - 15√3) ≈ √8,019238 ≈ 2,831826.
cosα = (5² + (34 - 15√3) - 9)/(2*5*√(34 - 15√3)) ≈ 0,848189.
Угол β = 31,98475 градуса.
Угол между векторами равен сумме углов α и β и равен 35,0958 градуса.
Площадь параллелограмма равна произведению длин векторов на синус угла между ними.
S = √(634 + 75√3)*√(34 - 15√3)*0,57495 = 45 кв. ед.