Предмет: Алгебра,
автор: 32Саша23
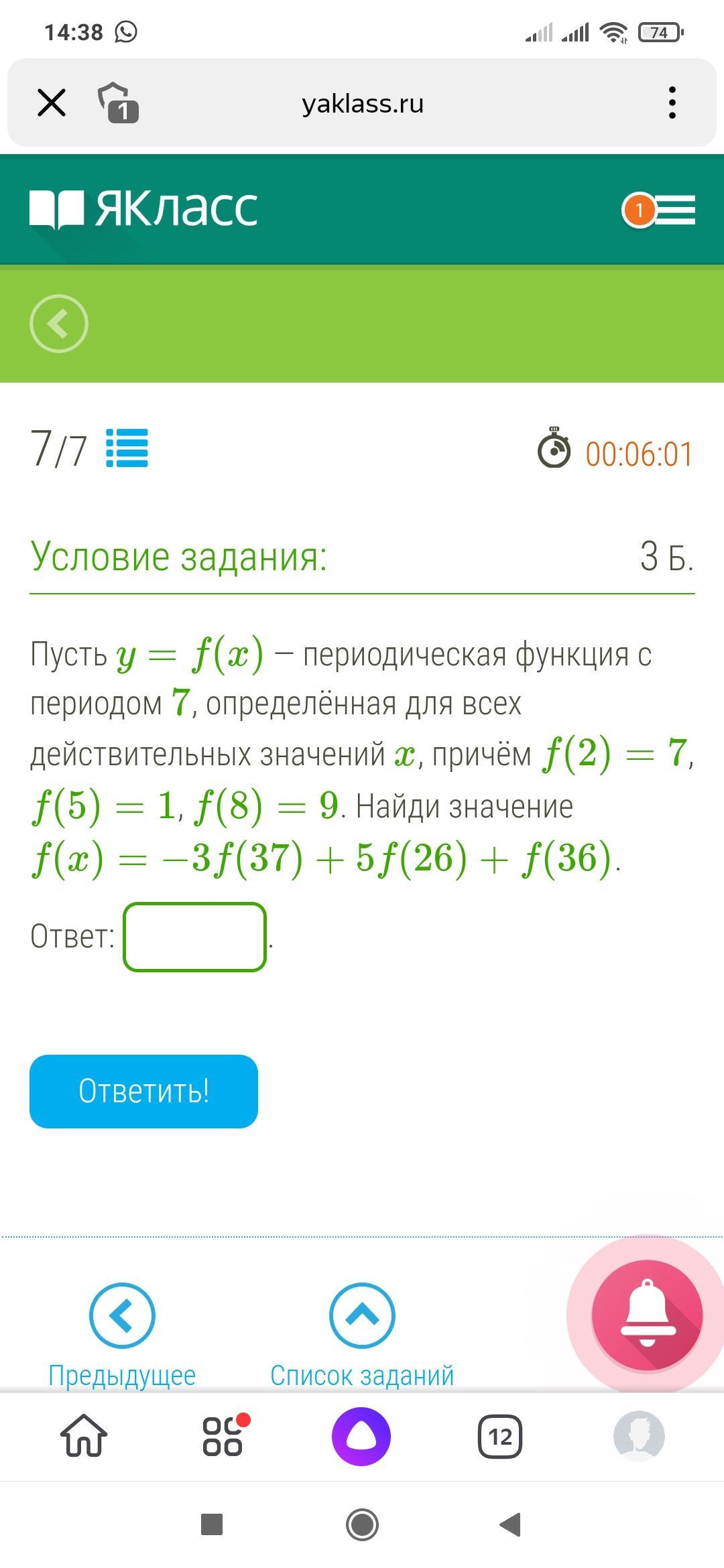
СРОЧНО !!!! Пусть y=f(x) — периодическая функция с периодом 7, определённая для всех действительных значений x, причём f(2)=7, f(5)=1, f(8)=9. Найди значение f(x)=−3f(37)+5f(26)+f(36).
Приложения:
Ответы
Автор ответа:
0
Ответ:
masha01021:
здравствуйте, помогите мне пожалуйста
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: Lomaron4ik
Предмет: Математика,
автор: Mishel12345
Предмет: Обществознание,
автор: lizaromanenko2
Предмет: Литература,
автор: cheskaanna