Предмет: Математика,
автор: retakeani2021
Добрый вечер. Помогите, пожалуйста, выполнить задание (Даю 10 баллов)
Приложения:
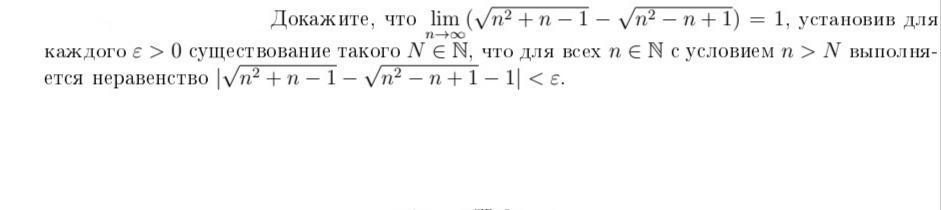
Ответы
Автор ответа:
1
Пусть произвольное задано. Домножая и деля на сопряженное выражение, получаем
(мы воспользовались тем, что поэтому знаменатель дроби больше 3/2, а также известным неравенством треугольника
Рассмотрим отдельно второй и третий модули.
Поэтому вся сумма меньше, чем (последнее неравенство в принципе лишнее, но ведь от нас не требуют делать оценку как можно точнее). Далее,
Поэтому в качестве N можно взять целую часть полученного числа:
, а если мы совсем зануды и не хотим получить N=0 при
то можем к ответу добавить еще единичку:
Замечание. Если я где-то ошибся в расчетах, сообщите мне, чтобы я имел возможность исправить ошибки.
Похожие вопросы
Предмет: Математика,
автор: valentink59
Предмет: Русский язык,
автор: Llol23
Предмет: Физика,
автор: физик777228
Предмет: Биология,
автор: 4fox4
Предмет: История,
автор: Воронежская1