Question

Даю много баллов + лучший ответ!
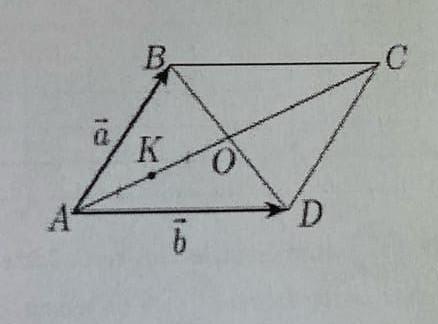
ABCD-параллелограмм, O - диагоналей AC и BD пересекаемая точка, K- отрезка АО серединная точка. Дано что АВ=а и AD=b. Выразите векторами a и b.
1) AOвекторы 2) DKвекторы

Помогите пожалуйста!​

Answer 1

Ответ:

Объяснение:

1.  по правилу параллелограмма   AB+AD=AC,  AO=1/2 AC (т. О делит диагонали пополам),  значит,  AO=1/2AB+1/2AD=1/2a +1/2 b

2.  по правилу тр-ка  DK=DA+AK,   DA= -b,  AK = 1/2 AO (по усл.),

AK=1/2 (1/2a+1/2b)=1/4a+1/4b,  тогда  DK=-b+1/4a+1/4b =1/4a-3/4b

Answer 2

Ответ:

1) (a + b) /2

2) (a - 3b) / 4

Объяснение:

→ - это вектор

1) →DB = →DA + →AB = -(→AD) + →AB = -b + a = a - b

→DO = →DB / 2 = (a - b) / 2

→AO = →AD + →DO = b + (a - b) / 2 = (2b + a - b) / 2 = (a + b) / 2

ИЛИ

→AB + →AD = →AC(→AD можно переместить на место →BC, чтобы было легче сложить векторы a и b)

Тогда →AO = →AC / 2 = (a + b) / 2

2) →DK = →DO + →OK = (a - b) / 2 + →OA / 2 =

(a - b) /2 + (-(→AO) / 2) = (a - b) / 2 + (-((a + b) / 2) / 2) = (a - b) / 2 - (a + b) / 4 = (2(a - b) - (a + b)) / 4 = (2a - 2b - a - b) / 4 = (a - 3b) / 4