Даю 39 балов все свои последние

Ответы
#1.
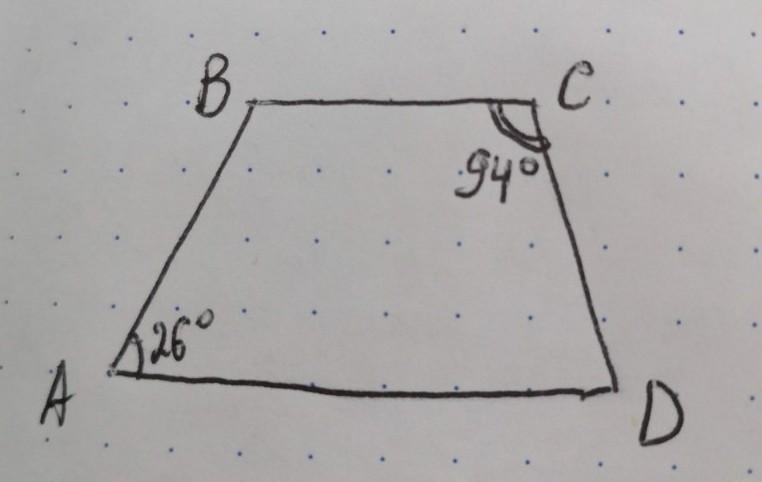
Дано:
трапеция ABCD,
∠A = 26°,
∠C = 94°
Найти: ∠B, ∠D
Решение:
Свойство, подходящее для трапеции любого вида: сумма углов, прилегающих к боковой стороне, равна 180°. (Также, можно воспользоваться Теоремой об углах, образованных двумя параллельными прямыми и секущей. Основания трапеции параллельны, это свойство самой трапеции, секущая — это боковая сторона. Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180°. Односторонние углы — ∠A и ∠B, ∠C и ∠D. Это, получается, доказательство вышеупомянутого свойства, необязательное, просто для информации)
Получается,
∠A + ∠B = 180°, ∠C + ∠D = 180°,
∠B = 180° – ∠A = 180° – 26° = 154°,
∠D = 180° – ∠C = 180° – 94° = 86°.
Ответ: ∠B = 154°, ∠D = 86°.
#2.
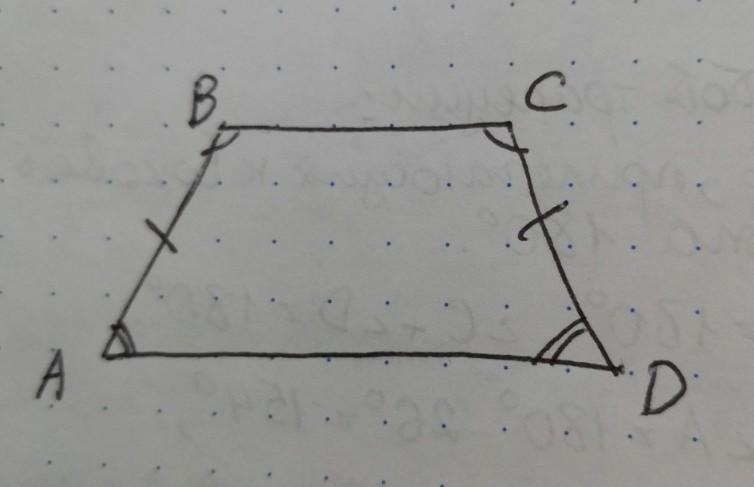
Дано:
равнобедренная трапеция ABCD, где BC и AD — основания трапеции,
∠B + ∠C = 240°
Найти: ∠A, ∠B, ∠C, ∠D
Решение:
Сумма углов трапеции (как и любого выпуклого четырёхугольника) равна 360°,
∠A + ∠B + ∠C + ∠D = 360°
(∠B + ∠C) + ∠A + ∠D = 360°
240° + ∠A + ∠D = 360°
∠A + ∠D = 120°.
В равнобедренной трапеции углы при основаниях попарно равны, то есть
∠B = ∠C, ∠A = ∠D.
Значит,
∠A + ∠A = 2 × ∠A = 120°,
∠D + ∠D = 2 × ∠D = 120°,
Получается,
∠A = ∠D = 120° ÷ 2 = 60°.
По условию, ∠B + ∠C = 240°,
Значит,
∠B + ∠B = 2 × ∠B = 240°,
∠C + ∠C = 2 × ∠C = 240°,
Получается,
∠B = ∠C = 240° ÷ 2 = 120°.
Ответ: ∠A = 60°, ∠B = 120°, ∠C = 120°, ∠D = 60°.