Предмет: Алгебра,
автор: Аноним
Вычислить площадь фигуры, ограниченной линиями.
Приложения:
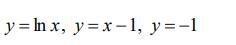
Ответы
Автор ответа:
2
Ответ:
Приложения:
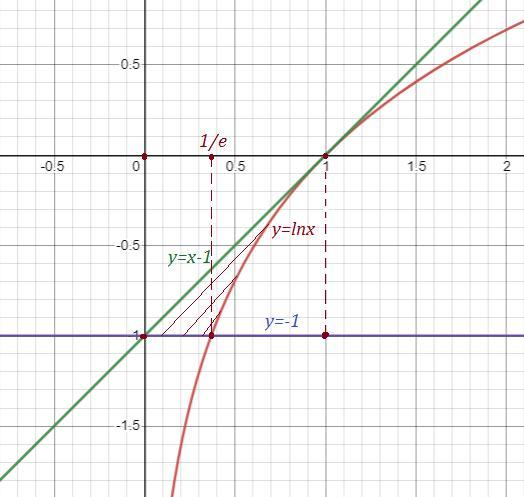
Похожие вопросы
Предмет: Русский язык,
автор: ВераКаплунова
Предмет: Русский язык,
автор: 1Илюха111111
Предмет: Русский язык,
автор: данил6664
Предмет: Алгебра,
автор: daria27144
Предмет: Алгебра,
автор: danilava
Можешь помочь с остальными заданиями?
https://znanija.com/task/45715721