Предмет: Алгебра,
автор: vityamath
решите два задания(как можно подробнее)
Приложения:

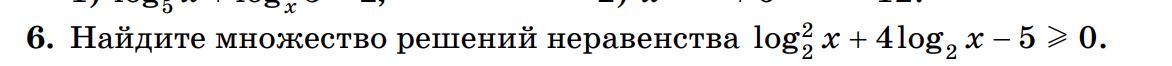
Ответы
Автор ответа:
0
(lg 300 - lg 3) / (3log(6) 2 + log(6) 27) = lg (300/3) / (log(6) 2³ + log(6) 3³) = lg 100 / log(6) 6³ = 2/3
log²(2) x + 4log(2) x - 5 ≥ 0
x > 0
log(2) x = y
y² + 4y - 5 ≥ 0
(y + 5)(y - 1) ≥ 0
+++++++[-5] ------------- [1] +++++++++
1. y ≤ -5
log(2) x ≤ 5
x ≤ 2^-5 = 1/32
2/ y ≥ 1
log(2) x ≥ 1
x ≥ 2
x ∈ (0, 1/32] U [2, +∞)
Автор ответа:
1
Ответ:
Объяснение:
Похожие вопросы
Предмет: Русский язык,
автор: oPel163228
Предмет: Русский язык,
автор: иринка114
Предмет: Русский язык,
автор: Орхидея111111
Предмет: Русский язык,
автор: Котвсапогах10
Предмет: Алгебра,
автор: Аноним