Question

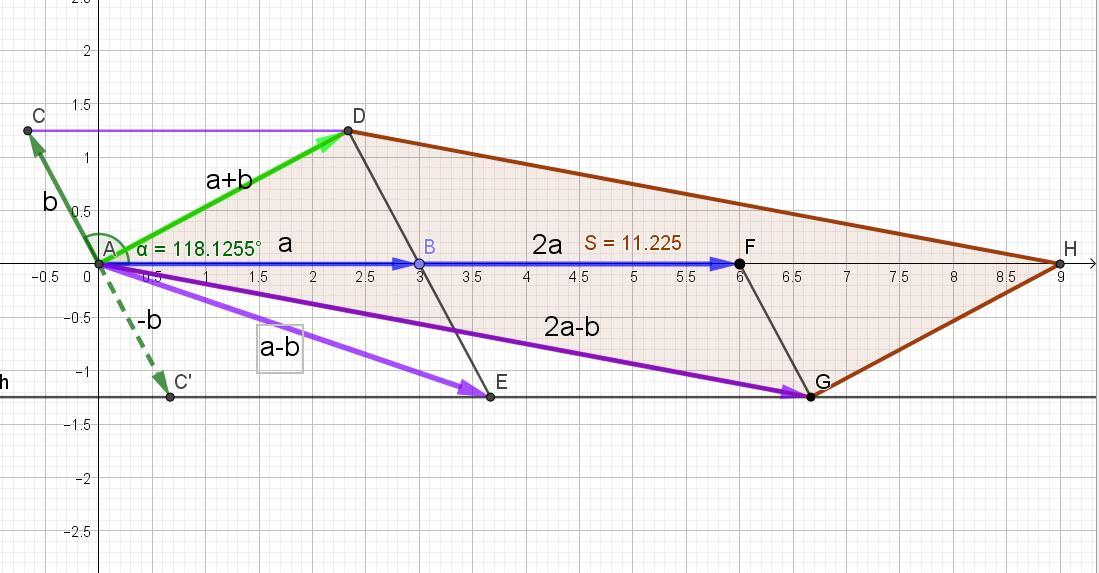
Найти скалярное произведение вектора (2a-b)*(a+b), если lal =3, l b l = sqrt(2) и la=bl = sqrt(15)

Answer 1

Даны векторы lal =3, l b l = sqrt(2), также будем считать , что дано

la-bl = sqrt(15).

Найти скалярное произведение векторов (2a-b) и (a+b).

Зная модули векторов и длину модуля их разности, можно по теореме косинусов найти угол между векторами.

cos A = (a² + |-b|² - |a-b|²)/(2*a*|-b|) = (9 + 2 - 15)/(2*3*√2) = -4/(6√2) = -√2/3.

Определяем модуль |a+b|.

|a+b| = √(a² + b² - 2*a*b*cosA) = √(9 + 2 - 2*3*√2*(-√2/3)) = √7.

Теперь можно найти угол наклона вектора |a+b| к оси Ох.

cos(DAB) = (9 + 7 - 2)/(2*3*√7) = 14/(6√7) = √7/3.

Этот угол равен 28,2551 градуса.

Находим модуль |2a-b| с учётом, что угол AFG равен углу А.

|2a-b| = √(36 + 2 - 2*6*√2*(-√2/3)) = √46.

Отсюда находим угол FAG наклона вектора |2a-b| к оси Ох.

cos(FAG) = (36 + 46 - 2)/(2*6*√46) = 80/(12√46) = 10√46/69.

Угол равен 10,59657 градуса.

Угол между векторами |2a-b| и |a+b| равен сумме:

∠(|2a-b|_|a+b|) = 28,2551 + 10,59657  = 38,72207 градуса.

Теперь можно подойти к решению задания: найти скалярное произведение вектора (2a-b)*(a+b).

Оно равно произведению длин этих векторов на косинус угла между ними.

Численно оно равно:

(2a-b)*(a+b) = √46*√7*cos 38,72207° = √322*0,78019 = 14.