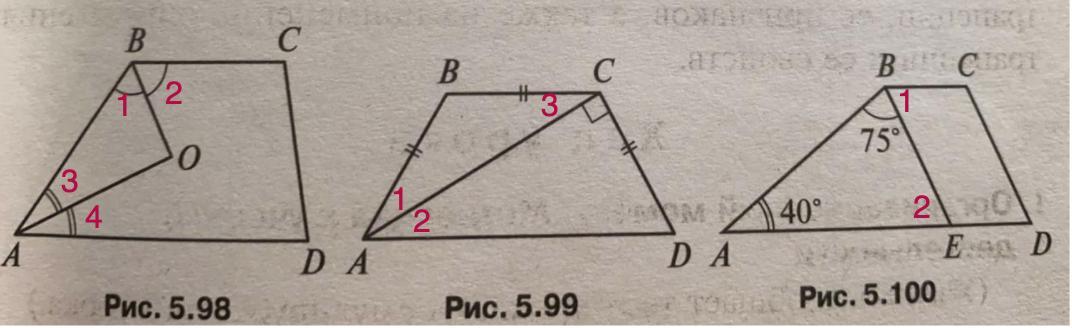
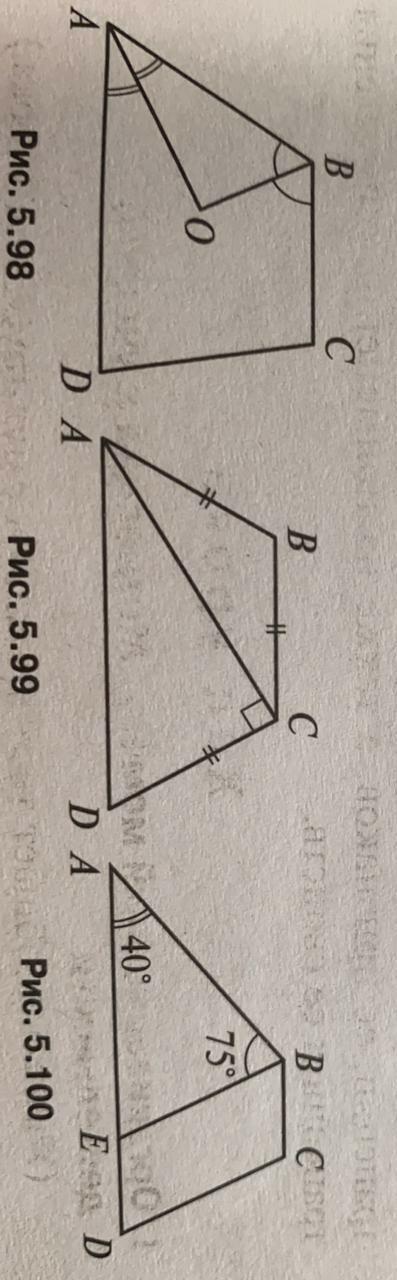
1.Дано: ABCD трапеция Найти: угол AOB(рис 5.98)
2.Дано: ABCD трапеция Найти:углы трапеции(рис 5.99)
3.Дано: ABCD трапеция, BE||CD Найти:углы трапеции(рис 5.100)
Ответы
Объяснение:
1. Дано: ABCD - трапеция;
АО и ВО - биссектрисы ∠А и ∠В соответственно.
Найти: ∠АОВ.
Решение:
- Углы трапеции, прилежащие к боковой стороне в сумме составляют 180°.
⇒ ∠А+∠В=180°
или ∠1+∠2+∠3+∠4=180°
Так как ∠1=∠2 (ВО - биссектриса)
и ∠3=∠4 (АО - биссектриса)
То получим
∠1+∠3=180°:2=90°
Рассмотрим ΔАВО.
- Сумма углов треугольника равна 180°.
⇒ ∠АОВ=180°-(∠1+∠3)=180°-90°=90°
2. Дано: ABCD - равнобедренная трапеция;
АВ=ВС; ∠АСD =90°
Найти: углы трапеции.
Решение:
Рассмотрим ΔАВС - равнобедренный (условие)
- Углы при основании равнобедренного треугольника равны.
⇒ ∠1=∠3
∠2=∠3 - накрест лежащие при ВС║AD и секущей АС.
⇒ ∠1=∠2
- Углы при основаниях равнобедренной трапеции равны.
⇒ ∠А=∠D.
Пусть ∠1=∠2=α, тогда ∠А=∠D=2α
Рассмотрим ΔАСD - прямоугольный.
- Сумма острых углов прямоугольного треугольника равна 90°.
⇒ α+2α=90° или α=30°
Имеем ∠А=∠D=2α=60°
- Углы трапеции, прилежащие к боковой стороне в сумме составляют 180°.
⇒ ∠В=∠С=180°-60°=120°
3. Дано: АВСD - трапеция.
ВЕ║СD
∠А=40°; ∠АВЕ=75°
Найти: углы трапеции.
Решение:
Рассмотрим ΔАВЕ.
- Сумма углов треугольника равна 180°.
⇒ ∠2=180°-(40°+75°)=65°
∠1=∠2=65° (накрест лежащие при ВС║АD и секущей ВЕ)
⇒ ∠В=75°+65°=140°
ВС║ЕD и ВЕ║СD (условие)
⇒ЕВСD - параллелограмм (по определению)
- Противоположные углы параллелограмма равны.
⇒ ∠D=∠1=65°
- Углы трапеции, прилежащие к боковой стороне в сумме составляют 180°.
⇒ ∠C =180°-∠D=180°-65°=115°