Предмет: Алгебра,
автор: kazakovaelizaveta056
Решите пожалуйста!!!!
Приложения:
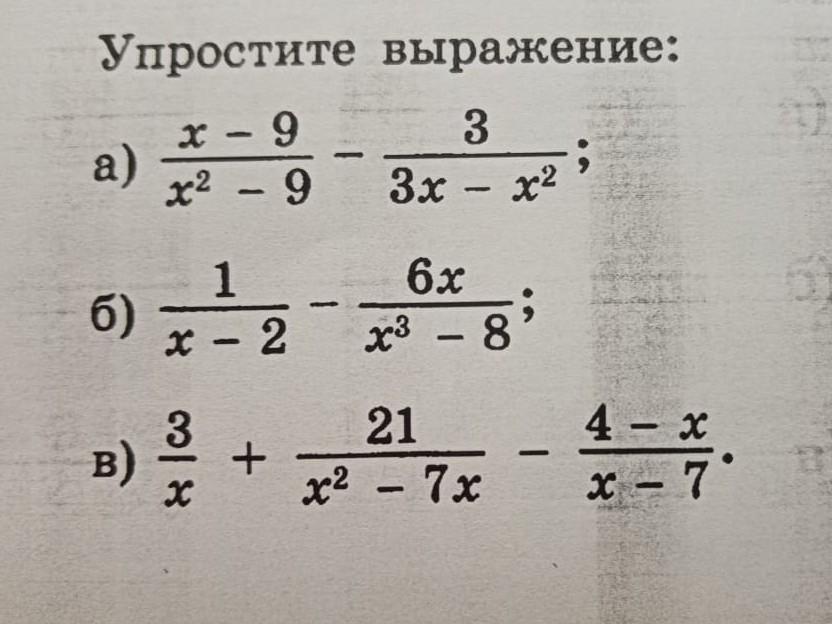
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Русский язык,
автор: 985416
Предмет: Русский язык,
автор: suzi1004
Предмет: Русский язык,
автор: натали260
Предмет: Геометрия,
автор: Muhtargav
Предмет: Математика,
автор: дочери20