Предмет: Геометрия,
автор: malarcukvika02
Відомо, що cos α = 4/5.
α лежить в І чверті.
Знайдіть sin α.
Ответы
Автор ответа:
1
Відповідь: 3/5
Пояснення: фото
Приложения:
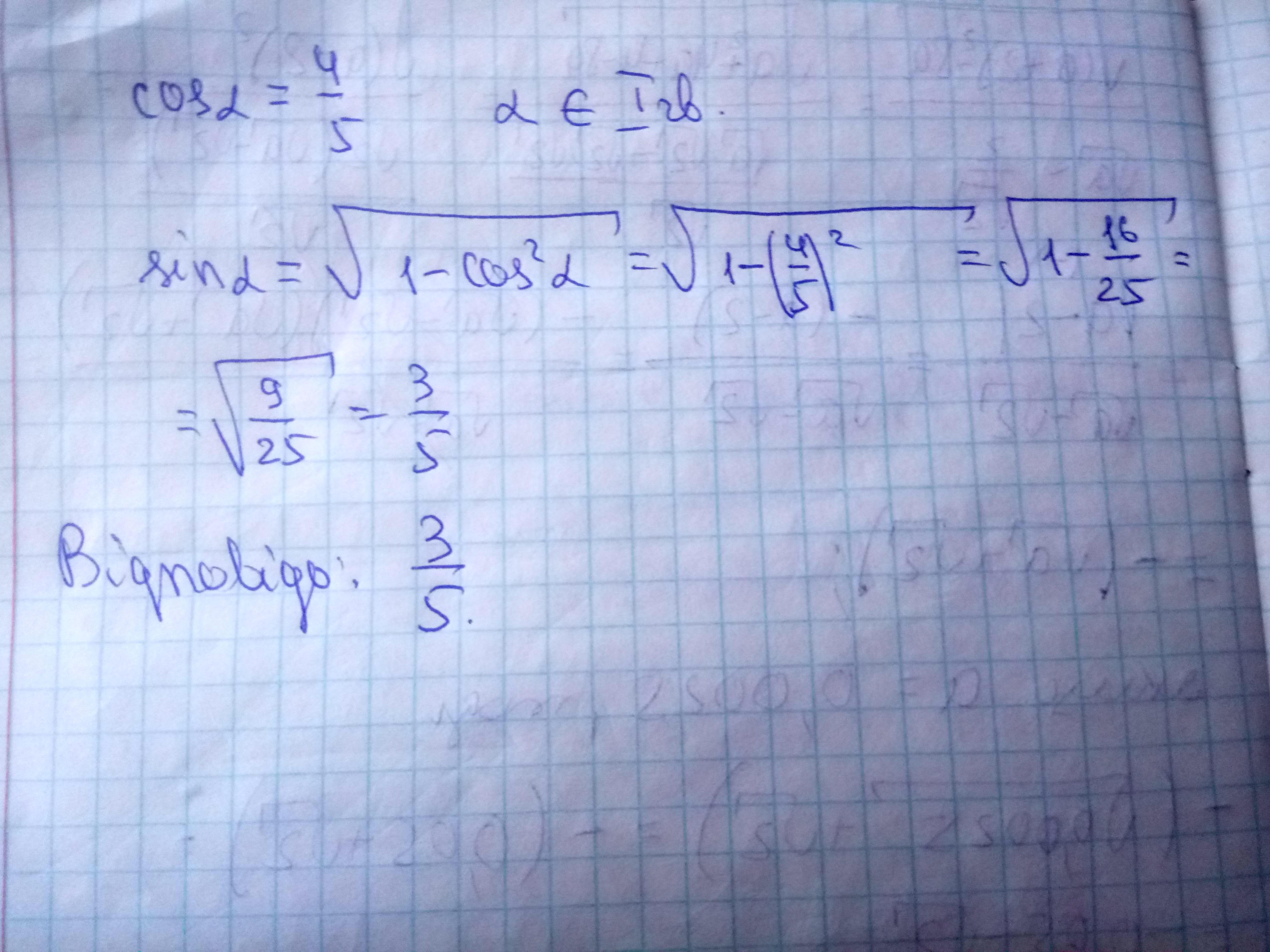
Автор ответа:
2
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: bazalilarisa
Предмет: Русский язык,
автор: Хмзо
Предмет: Английский язык,
автор: Polinochka2005
Предмет: Математика,
автор: изабелла29
Предмет: Математика,
автор: aljonafilatova