Предмет: Математика,
автор: bogdana8516
Пожалуйста помогите с примером:
Приложения:
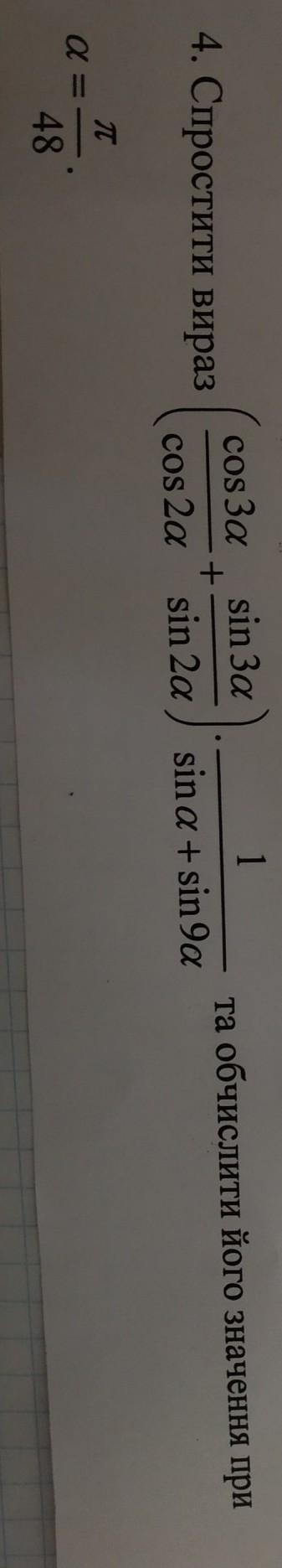
Ответы
Автор ответа:
0
Пошаговое объяснение:
Конечную форму можно отредактировать следующим образом:
При значении выражение будет равно:
Похожие вопросы
Предмет: Русский язык,
автор: 333Лиза44
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: варя731
Предмет: Химия,
автор: Даня7677
Предмет: Математика,
автор: EvilSd