Question

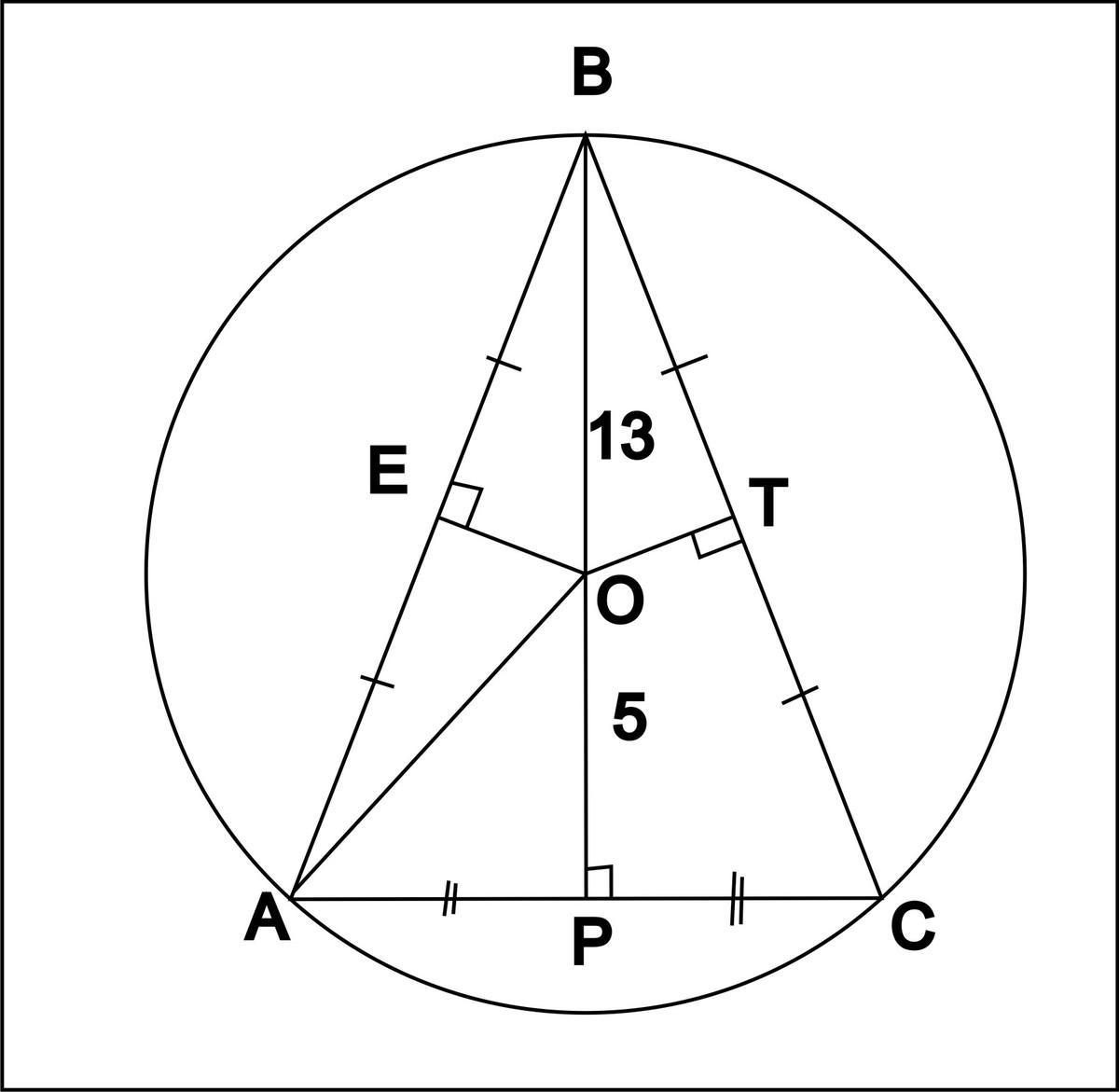
центр описанной окружности лежит на высоте разнобедренного треугольника и делит высоту на отрезки, равны 5 см и 13 см. Найдите площадь этого треугольника ​

Answer 1

центр описанной около треугольника окружности лежит на пересечении серединных перпендикуляров

центр описанной около треугольника окружности лежит на пересечении серединных перпендикуляров

ВО=ОА=13= радиусу описанной окружности

по теореме Пифагора

АР^2=AO^2-OP^2

AP=12

площадь треугольника равна половине высоты на основание

S=(1/2)*BP*AC=18*12=216

Ещё могу прикрепить фото