Предмет: Математика,
автор: jakegriffin1
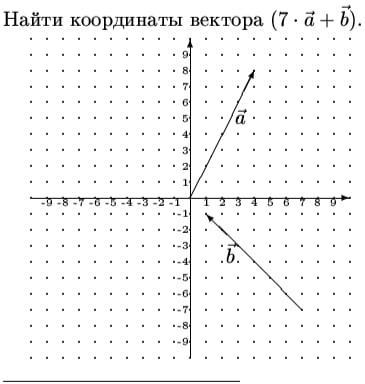
Помогите решить задание по математике.
Приложения:
Ответы
Автор ответа:
2
Ответ:
Пошаговое объяснение:
Вспоминаем
правило:
- чтобы найти координаты вектора AB, зная координаты его начальной точек А(х₀, у₀) и конечной точки В(х₁, у₁), необходимо из координат конечной точки вычесть соответствующие координаты начальной точки. AB={x₁-x₀; y₁-y₀}
правило:
- произведение ненулевого вектора на число - это вектор, координаты которого равны соответствующим координатам данного вектора, умноженным на число
правило:
- сложение векторов (сумма векторов)
есть операция вычисления вектора
, все элементы которого равны попарной сумме соответствующих элементов векторов
и
, то есть каждый элемент вектора c равен
Сначала найдем векторы и
.
Искать будем по двум точкам - начало и конец вектора.
Вектор : начало в т. (0; 0), конец (4; 8), тогда вектора а будет
Вектор : начало в т. (7; 7), конец (1; 1), тогда вектора b будет
А теперь можем найти координаты вектора .
Мы сразу будем искать и , и
Похожие вопросы
Предмет: Русский язык,
автор: euu
Предмет: Русский язык,
автор: 23021986
Предмет: Английский язык,
автор: алекс219
Предмет: Русский язык,
автор: lena152637
Предмет: Алгебра,
автор: DiAnNa123er