Question

1. Функция задана формулой y = -4x2 - 3x -1.

1.1. Найдите y(-3).

1.2. Определите при каких значениях аргумента значение функции равно -2.

1.3. Принадлежит ли графику функции точка A (-1; -2)?


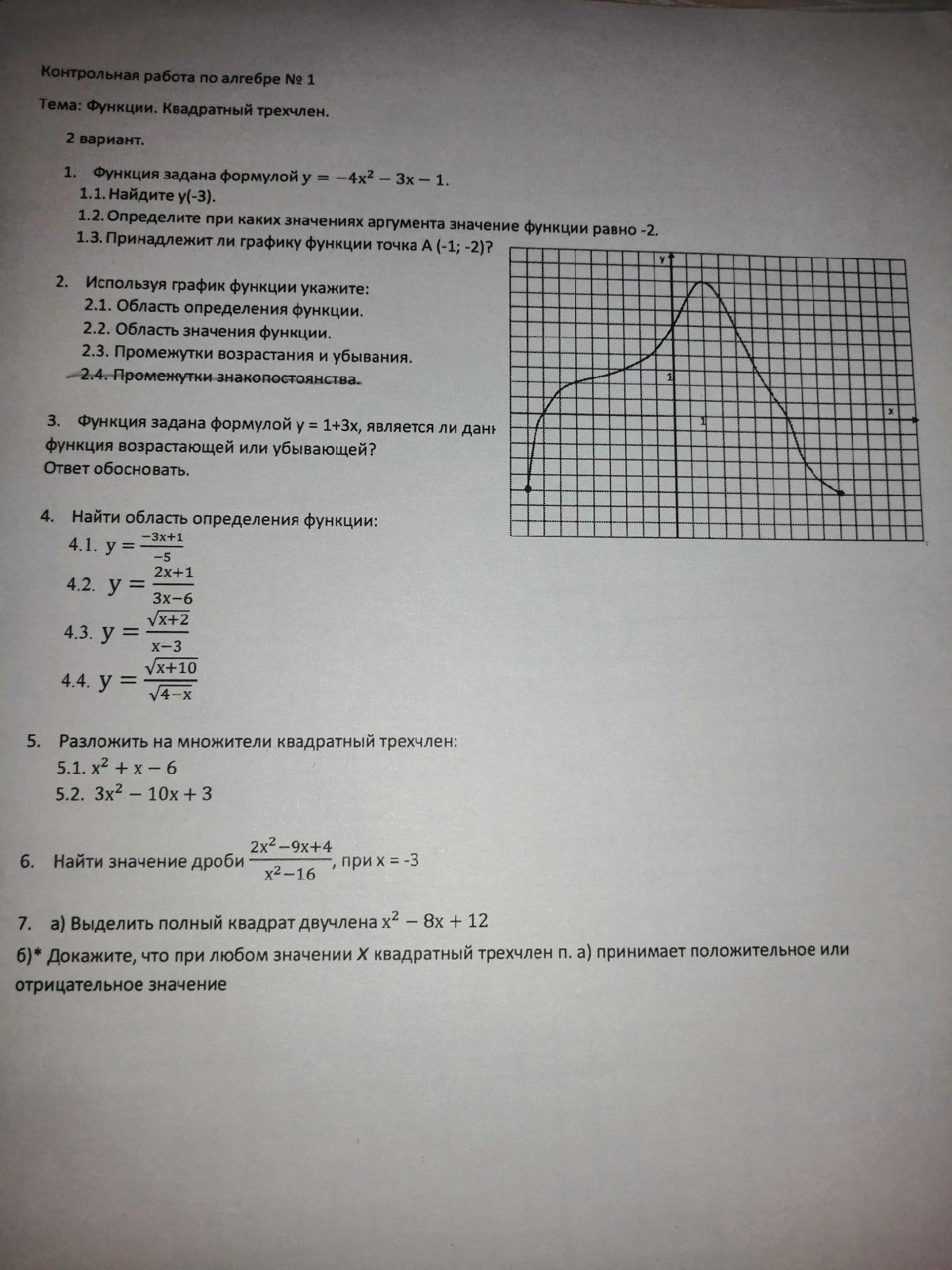
2. Используя графику функции укажите:

2.1. Область определения функции.

2.2. Область значения функции.

2.3. Промежутки возрастания и убывания


3. Функция задана формулой y = 1+3x, является ли данная функция возрастающей или убывающей? Ответ обосновать.


4. Найти область определения функции :

4.1. y = -3+1/-5

4.2. y = 2x+1/3x-6

4.3. y = √x+2/x-3

4.4. y = √x+10/√4-x


5. Разложить на множители квадратный трехчлен:

5.1. x^2 + x - 6

5.2. 3x^2 - 10x + 3


6. Найти значение дроби 2x^2-9x+4/x^2-16, при x = -3

Answer 1

#1. Функция задана формулой

$y = - 4 {x}^{2} - 3x - 1$

1.1 $y( - 3) = - 4 \times {( - 3)}^{2} - 3 \times ( - 3) - 1 = - 4 \times 9 + 9 - 1 = - 36 + 8 = - 28$

1.2 $- 2 = - 4 {x}^{2} - 3x - 1$

$4 {x}^{2} + 3x - 1 = 0$

$D = {b}^{2} - 4ac = 9 + 16 = 25$

$x_1 = \frac{ - b + \sqrt{D} }{2a} = \frac{ - 3 + 5}{2 \times 4} = \frac{2}{8} = \frac{1}{4}$

$x_2 = \frac{ - b - \sqrt{D} }{2a} = \frac{ - 3 - 5}{2 \times 4} = \frac{ - 8}{8} = - 1$

1.3 x = - 1, y = - 2, подставляем значения в функцию, если равенство будет верным, то значит точка А(-1; - 2) принадлежит графику функции. (в 1.2 мы нашли корни уравнения, при y=-2, x=-1, значит точка принадлежит графику функции, но, всё же, распишу так: )

$- 2 = - 4 \times {( - 1)}^{2} - 3 \times ( - 1) - 1$

$- 2 = - 4 + 3 - 1$

$- 2 = - 2$

равенство верное, точка принадлежит графику функции.

#2. Используя график функции укажите:

2.1 Область определения функции: [-4.5; 5]

2.2 Область значения функции: [-2.5; 4.5]

2.3 Промежутки возрастания функции: [-4.5; 1], промежутки убывания функции: [1; 5]

#3. $y = 1 + 3x$.

Это линейная функция, формула которой $y = kx + b$, где

если k > 0, то функция возрастающая, если k < 0, то функция убывающая.

У нас k = 3, 3 > 0 => функция возрастающая.

#4. Найти область определения функции:

4.1 $y = \frac{ - 3x + 1}{ - 5}$

Область определения: $( - \infty ; + \infty )$

4.2 $y = \frac{2x + 1}{3x - 6}$

знаменатель не должен быть равным нулю: $3x - 6≠0$, $3x≠6$, $x≠2$

Область определения: $( - \infty ; 2) \cup (2; + \infty )$

4.3 $y = \frac{ \sqrt{x + 2} }{x - 3}$

в числителе корень, число под корнем не должно быть отрицательным: $x + 2 \geqslant 0$, $x \geqslant - 2$

знаменатель не должен быть равным нулю: $x-3≠0$, $x≠3$

Область определения: $[ -2; 3) \cup (3; + \infty )$

4.4 $y = \frac{ \sqrt{x + 10} }{ \sqrt{4 - x} }$

в числителе корень, число под корнем не должно быть отрицательным: $x + 10 \geqslant 0$, $x \geqslant - 10$

в знаменателе корень, число под корнем не должно быть отрицательным; знаменатель не должен быть равным нулю: $4-x> 0$, $x < 4$

Область определения: $[ -10; 4)$

#5. Разложить на множители квадратный трёхчлен. Можно это сделать по формуле $a {x}^{2} + bx + c = a(x - x_1)(x - x_2)$, где $x_1$ и $x_2$ — корни уравнения $a {x}^{2} + bx + c = 0$.

5.1 ${x}^{2} + x - 6 = (x - 2)(x + 3)$

Решение:

${x}^{2} + x - 6 = 0$

$D = {b}^{2} - 4ac = 1 + 24 = 25$

$x_1 = \frac{ - b + \sqrt{D} }{2a} = \frac{ - 1 + 5}{2 \times 1} = \frac{4}{2} = 2$

$x_2 = \frac{ - b - \sqrt{D} }{2a} = \frac{ - 1 - 5}{2 \times 1} = \frac{ - 6}{2} = - 3$

5.2 $3 {x}^{2} - 10x + 3 = 3(x - 3)(x - \frac{1}{3} ) = (x - 3)(3x - 1)$

Решение:

$3 {x}^{2} - 10x + 3 = 0$

$D = {b}^{2} - 4ac = {( - 10)}^{2} - 4 \times 3 \times 3 = 100 -36 = 64$

$x_1 = \frac{ - b + \sqrt{D} }{2a} = \frac{10 + 8}{2 \times 3} = \frac{18}{6} = 3$

$x_2 = \frac{ - b - \sqrt{D} }{2a} = \frac{10 - 8}{2 \times 3} = \frac{2}{6} = \frac{1}{3}$

#6. Найти значение дроби $\frac{ 2 {x}^{2} - 9x + 4 }{ {x}^{2} - 16}$ при $x = - 3$.

Для начала нужно упростить дробь.

Разложим квадратный трёхчлен из числителя на множители, по формуле из задания 5.

$2 {x}^{2} - 9x + 4 = 0$

$D = {b}^{2} - 4ac = {(-9)}^{2} -4 \times 2 \times 4 = 81 - 32 = 49$

$x_1 = \frac{ - b + \sqrt{D} }{2a} = \frac{9 + 7}{2 \times 2} = \frac{16}{4} = 4$

$x_2 = \frac{ - b - \sqrt{D} }{2a} = \frac{9 - 7}{2 \times 2} = \frac{2}{4} = \frac{1}{2}$

$2 {x}^{2} - 9x + 4 = 2(x - 4)(x - \frac{1}{2}) = (x-4)(2x-1)$

В знаменателе разность квадратов, используем формулу сокращенного умножения.

${x}^{2} - 16 = {x}^{2} - {4}^{2} = (x-4)(x+4)$

В итоге,

$\frac{ 2 {x}^{2} - 9x + 4 }{ {x}^{2} - 16} = \frac{(x-4)(2x-1)}{(x-4)(x+4)} = \frac{2x-1}{x+4} = \frac{2 \times (-3) -1}{-3+4} = \frac{-7}{1} = - 7$

#7. а) ${x}^{2} - 8x + 12 = {x}^{2} - 2 \times 4 \times x + {4}^{2} + (12 - {4}^{2}) = {x}^{2} - 2 \times 4 \times x + {4}^{2} - 4 = {(x - 4)}^{2} - 4$