Предмет: Алгебра,
автор: kristinabulatova
распишите подробно решение.
Приложения:
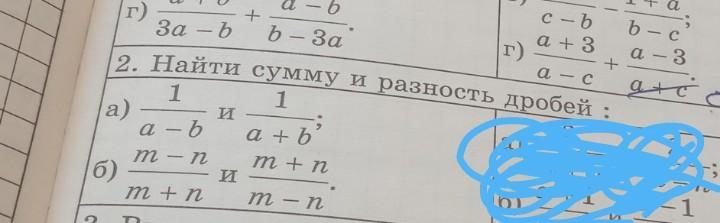
Ответы
Автор ответа:
0
a)
б)
Похожие вопросы
Предмет: Окружающий мир,
автор: зорро4
Предмет: Английский язык,
автор: русский132
Предмет: Английский язык,
автор: Космос1111111
Предмет: Математика,
автор: dinachugreeva
Предмет: Литература,
автор: 13191277