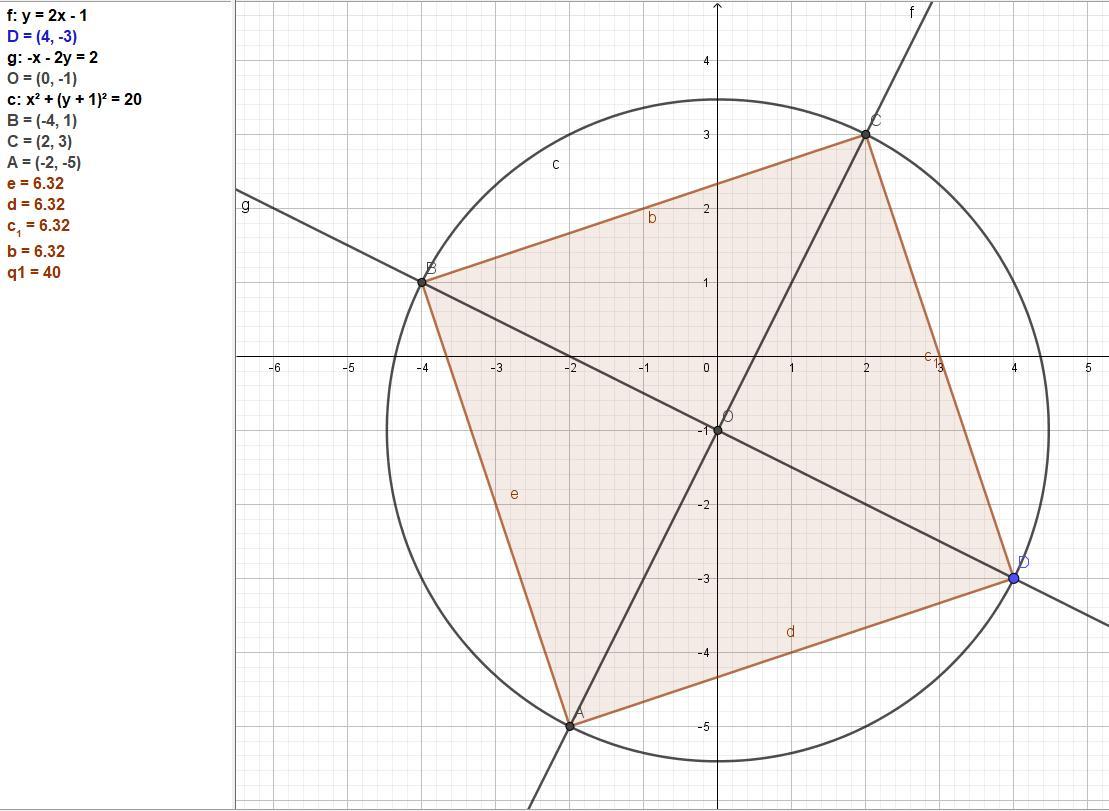
Диагональ квадрата расположена на прямой y=2x-1. Одна из его вершин находиться в точке в точке (4;-3). Составить уравнения его сторон и второй диагонали.
Ответы
Даны прямая y=2x - 1 (диагональ d1 квадрата) и точка (4; -3).
Эта точка не лежит на заданной прямой (2*4 - 1 ≠ -3).
Пусть это точка D (4; -3).
На перпендикуляре из точки D на заданную диагональ будет находиться вторая диагональ d2 квадрата.
Угловой коэффициент прямой d2 равен: k(d2) = -1/(k(d1)) = -1/2.
Уравнение d2: у = (-1/2)х + b. Для определения параметра d подставим координаты точки D: -3 = (-1/2)*4 + b. Отсюда b = -3 + 2 = -1.
Получили уравнение второй диагонали d2:
y = (-1/2)x - 1.
Далее используем формулу суммы тангенсов углов наклона прямой к оси Ох, так как этот тангенс является угловым коэффициентом прямой.
Угол между диагональю и стороной равен 45 градусов, его тангенс равен 1.
k(CD) = (2 + 1) / (1 - 2*1) = 3(-1) = -3.
Уравнение CD: y = -3x + b, для определения b подставим координаты точки D, через которую проходит прямая.
-3 = -3*4 + b, b = - 3+ 12 = 9.
Уравнение стороны CD: y = -3x + 9.
Пересечением диагонали и стороны CD найдём координаты точки С.
2х - 1 = -3х + 9, 5х = 10, х = 10/5 = 2, у = 2*2 - 1 = 3.
Точка С(2; 3).
Находим угловые коэффициенты уравнений двух других сторон квадрата как перпендикуляров.
k(BC) = k(AD) = -1/(-3) = 1/3.
Уравнение ВС: у = (1/3)х + b, подставим координаты найденной точки С.
3 = (1/3)*2 + b, b = 3 - (2/3) = 7/3.
Уравнение стороны BC: y = (1/3)x + (7/3).
Определяем уравнение стороны AD, у которой угловой коэффициент равен таковому стороны ВС.
Уравнение AD: у = (1/3)х + b, подставим координаты заданной точки D.
-3 = (1/3)*4 + b, b = -3 - (4/3) = -13/3.
Уравнение стороны AD: y = (1/3 - (13/3).
Определим координаты точки В пересечением диагонали d2 и стороны ВС.
(-1/2)х - 1 = (1/3)х + (7/3), (5/6)х = -10/3, х = (-10/3)/(5/6) = -4,
у =(-1/2)*(-4) - 1 = 1.
Точка B(-4; 1).
Определяем уравнение стороны AВ, у которой угловой коэффициент равен таковому стороны CD.
Уравнение AB: у = -3х + b, подставим координаты найденной точки B.
1 = -3*(-4) + b, b = 1 - 12 = -11.
Уравнение стороны AB: y = -3x - 11.