Розв'яжіть задачу.
Бісектриса тупого кута паралелограма ділить його більшу сторону на вiдрiзки, один із яких, прилеглий до вершини гострого кута, на 1,2 см більший за інший. Знайдіть сторони паралелограма, якщо його периметр дорівнює 13,8 см.
Будь ласка можна з :Дано: Знайти: Розв'язок: А також малюнок)))
Ответы
Дано:
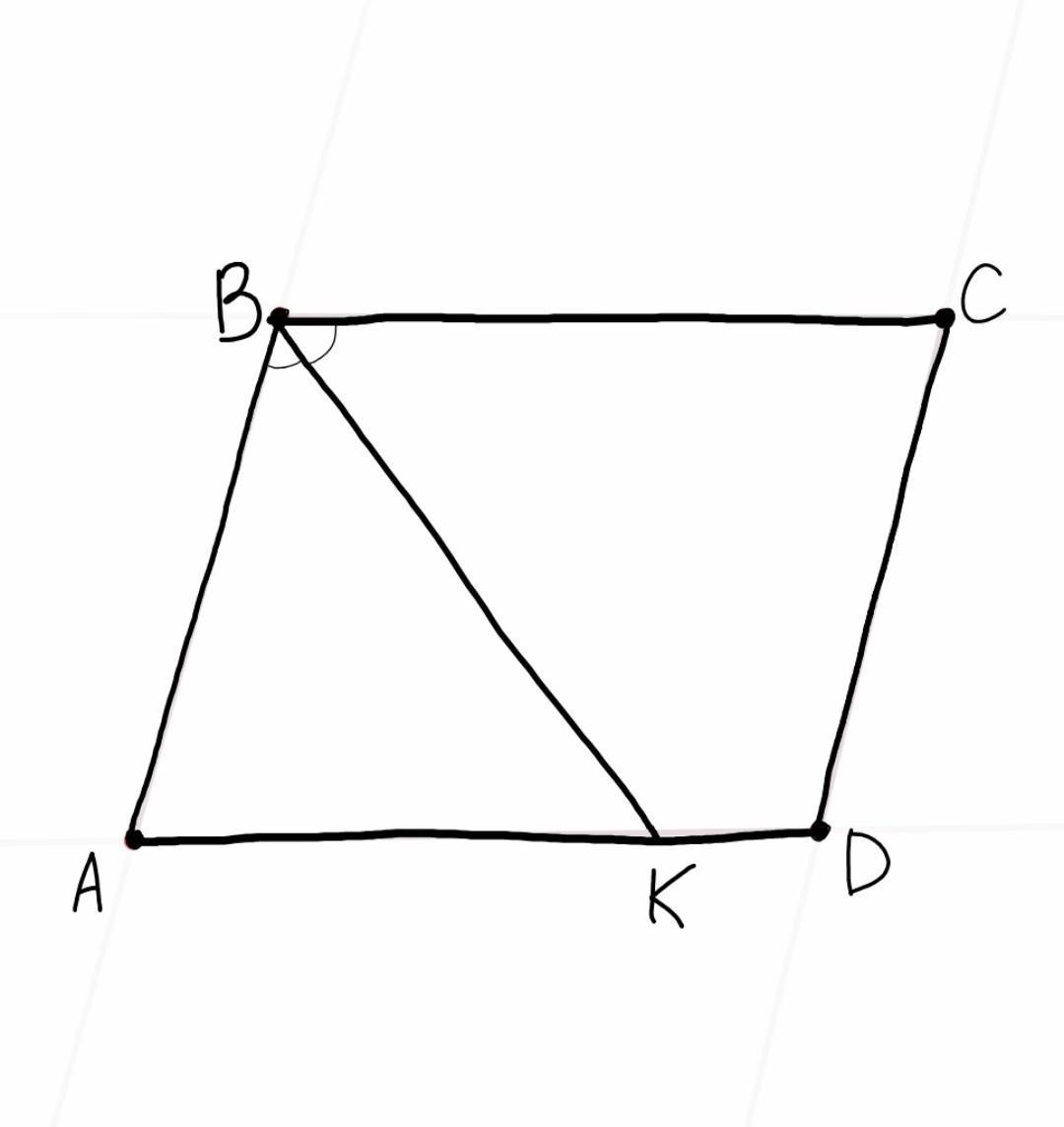
параллелограмм ABCD
BK — биссектриса ∠ABC
AK = KD + 1.2 см
[tex] P_{ABCD} [\tex] = 13.8 см
Найти: AB, BC, CD, AD
Решение:
Биссектрисса параллелограмма отсекает от него равнобедренный треугольник, это дополнительное свойство параллелограмма. (Это не обязательно, но: Вытекает оно из теоремы об углах, образованных двумя параллельными прямыми и секущей. Противоположные стороны параллелограмма параллельны, это свойство параллелограмма, то есть, AD || BC, а BK — секущая. Получается, что ∠CBK и ∠AKB — внутренние накрест лежащие углы, а они равны, то есть, ∠CBK = ∠AKB. BK — биссектриса ∠ABC, ∠ABK = ∠CBK, значит ∠ABK = ∠AKB и получается, что у треугольника ABK два угла равны, значит треугольник ABK — равнобедренный).
Треугольник ABK — равнобедренный, углы при основании равны, ∠ABK = ∠AKB. У равнобедренного треугольника боковые стороны равны, AB = AK.
Противоположные стороны параллелограмма попарно равны, AB = CD, BC = AD. Периметр параллелограмма равен удвоенной сумме двух его смежных сторон,
[tex] P_{ABCD} [\tex] = 2 × (AB + AD) = 13.8 см,
AB + AD = 13.8 см ÷ 2 = 6.9 см.
AK = KD + 1.2 см, по условию задачи =>
AB = AK = KD + 1.2 см;
AD = AK + KD = KD + 1.2 см + KD = 2×KD + 1.2 см;
AB + AD = KD + 1.2 см + 2×KD + 1.2 см = 3×KD + 2.4 см = 6.9 см,
3×KD = 6.9 см – 2.4 см = 4.5 см,
KD = 4.5 см ÷ 3 = 1.5 см. =>
AB = CD = KD + 1.2 см = 1.5 см + 1.2 см = 2.7 см,
BC = AD = 2×KD + 1.2 см = 2 × 1.5 см + 1.2 см = 3 см + 1.2 см = 4.2 см
Ответ: AB = 2.7см, BC = 4.2см, CD = 2.7см, AD = 4.2см