Предмет: Алгебра,
автор: arkadey234
Хелп плиз гайс . Упростите:
Приложения:
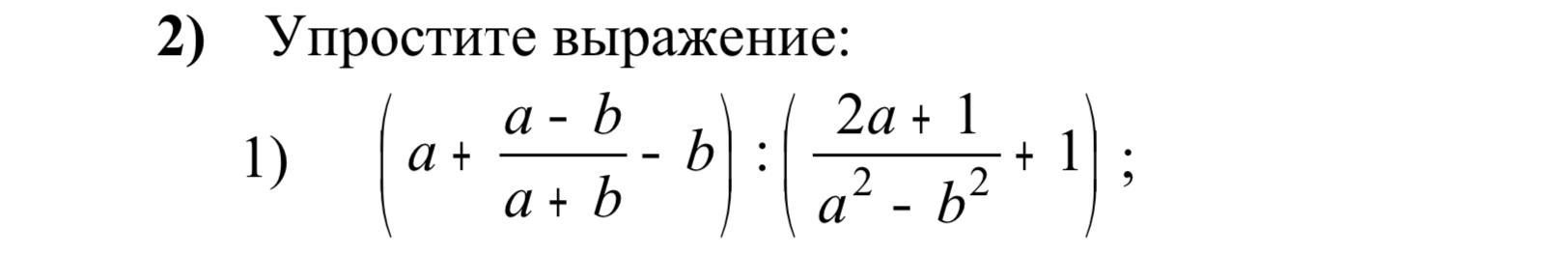
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Похожие вопросы
Предмет: Русский язык,
автор: Ама1111
Предмет: Английский язык,
автор: AlisaShab
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: Котейка0503