Предмет: Геометрия,
автор: 2007Makaroni
Задача 10. Вершину параллелограмма со- единили с серединами двух его проти- воположных сторон. Могут ли три от- меченные на рисунке угла быть равными друг другу?
Приложения:

Ответы
Автор ответа:
10
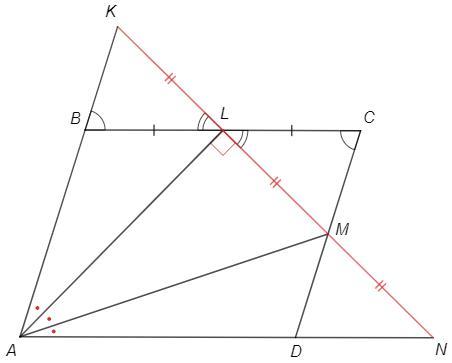
L, M - середины сторон.
Продлим LM до пересечения с AB в точке K
BL=LC (по условию)
∠KBL=∠C (накрест лежащие при AB||CD)
∠KLB=∠MLC (вертикальные)
△KBL=△MCL (по стороне и прилежащим углам) => KL=LM
△KAM: AL - биссектриса (по условию) и медиана, следовательно и высота, ∠ALM=90.
Продлим LM до пересечения с AD в точке N
Рассуждая аналогично, △MDN=△MCL => MN=LM =>
△NAL: AM - биссектриса/медиана, следовательно и высота, ∠AMN=90
Из точки A можно провести только один перпендикуляр к прямой LM. Следовательно данная конфигурация невозможна.
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: mad13
Предмет: Русский язык,
автор: 0Happy0
Предмет: Русский язык,
автор: На100я
Предмет: Русский язык,
автор: Betyshka
Предмет: Химия,
автор: alina02071