Предмет: Алгебра,
автор: Аноним
помогите, пожалуйста! Найти область сходимости степенного ряда.
Приложения:
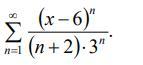
Ответы
Автор ответа:
1
Ответ:
ряд условно сходится (по признаку Лейбница) .
Похожие вопросы
Предмет: Окружающий мир,
автор: Артур111000
Предмет: Українська література,
автор: Настюня11111душка
Предмет: Русский язык,
автор: дяма
Предмет: Математика,
автор: Аноним
можешь тут помочь, пожалуйста!
https://znanija.com/task/45676559