Помогите пожалуйста! Номер 17.13!

Ответы
Ответ:
Sбок.пов=144√2(см²)
Объяснение:
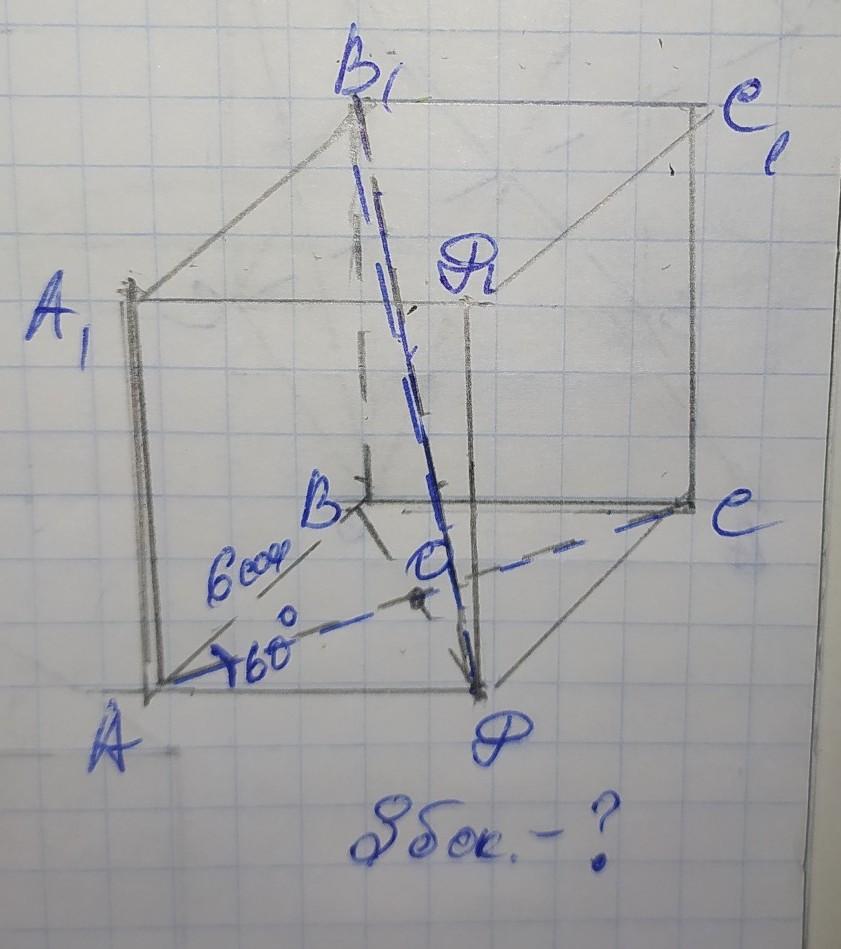
Обозначим вершины параллелепипеда АВСДА₁В₁С₁Д₁, диагонали и в основании АС и ВД и точкой их пересечения О, при этом АС – большая диагональ основания, а В₁Д – меньшая диагональ параллелепипеда. Диагонали ромба, пересекаясь под прямым углом, делятся пополам, образуя равные прямоугольные треугольники, а также делят углы пополам, из которых проведены, поэтому АО=ОС и ВО=ОД, ∠ВАО=∠ДАО=60÷2=30°. Рассмотрим ∆АВО. В нём АО и ВО – катеты, а АВ – гипотенуза. Катет ВО лежит напротив ∠ВАО=30°, значит он равен половине гипотенузы АВ:
ВО=АВ÷2=6÷2=3(см), тогда диагональ ВД=3×2=6см.
Найдём по теореме Пифагора катет АО:
АО²=АВ²–ВО²=6²–3²=36–9=27;
АО=√27=3√3(см).
Тогда большая диагональ АС=3√3×2=6√3(см).
Так как меньшая диагональ параллелепипеда равна большей диагонали основания, то
В₁Д=АС=6√3(см).
Рассмотрим ∆В₁ДВ. Он прямоугольный с катетами ВД и ВВ₁ и гипотенузой В₁Д. Найдём высоту ВВ₁ по теореме Пифагора:
ВВ₁²=В₁Д²–ВД²=(6√3)²–6²=36×3–36=
=36(3–1)=36×2=72;
ВВ₁=√72=6√2(см).
Найдём площадь одной боковой грани АА₁В₁В:
Sбок.гр.=ВВ₁×АВ=6√2×6=36√2(см²).
Так как в основанили лежит ромб, у которого все стороны равны, то все боковые грани будут одинаковой площади, и поскольку их 4, тогда, площадь боковой поверхности равна:
Sбок.пов.=36√2×4=144√2(см²)