Предмет: Алгебра,
автор: svinoboyanna2
Изобразите множество точек, заданных системой неравенств:
Приложения:
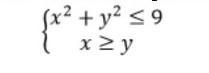
Ответы
Автор ответа:
4
Объяснение:
1). окружность с центром в точке О(0;0) и радиусом R=3. неравенство нестрогое, => окружность сплошная. заштриховать внутренность окружности.
2). прямая у=х, биссектриса I и III координатных углов. прямая сплошная, заштриховать полуплоскость ниже прямой.
ответ во вложении:
пересечение штриховок:
полукруг+отрезок прямой - диаметр окружности(красным цветом)
Приложения:

EmilyFortlander:
Спасибо
Похожие вопросы
Предмет: Окружающий мир,
автор: кристина797
Предмет: Русский язык,
автор: Настя045
Предмет: Русский язык,
автор: никита1158
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: LenaMonina1355