Предмет: Алгебра,
автор: Аноним
Помогите пожалуйста решить
Приложения:
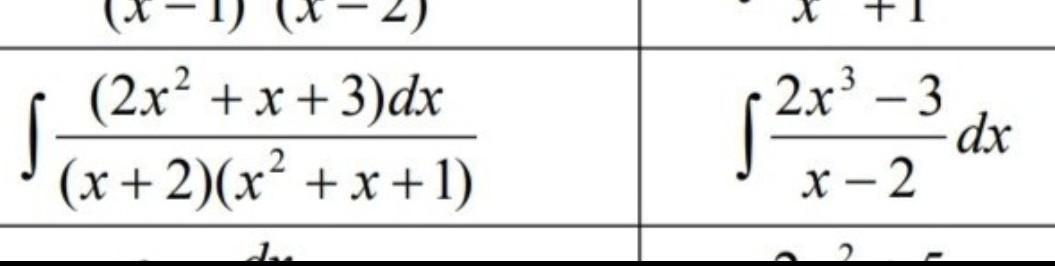
Ответы
Автор ответа:
0
Ответ:
Объяснение:
первый интеграл
разложим его на простейшие дроби
теперь первый снова разложим
замена для первого интеграла [u=x²+x+1 du=(2x+1)dx ]
теперь остался второй интеграл. надо добиться в знаменателе x² +a²
сначала выделим полный квадрат а потом будем выносить за скобки множители
теперь сделаем обратную подстановку и получим
- это ответ
второй интеграл
здесь надо просто поделить многочлен на многочлен и тогда получим сумму простых интегралов
Похожие вопросы
Предмет: Русский язык,
автор: Tori163
Предмет: Русский язык,
автор: inna2900
Предмет: Русский язык,
автор: лера744
Предмет: Алгебра,
автор: olga241189ллылылды
Предмет: Математика,
автор: Faust1014