Предмет: Алгебра,
автор: denis232515
даю 100 балов
срочно
Приложения:
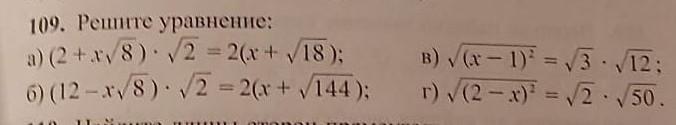
Ответы
Автор ответа:
1
Ответ:
Автор ответа:
1
Объяснение:
дрежи))))))))))))))))
Приложения:


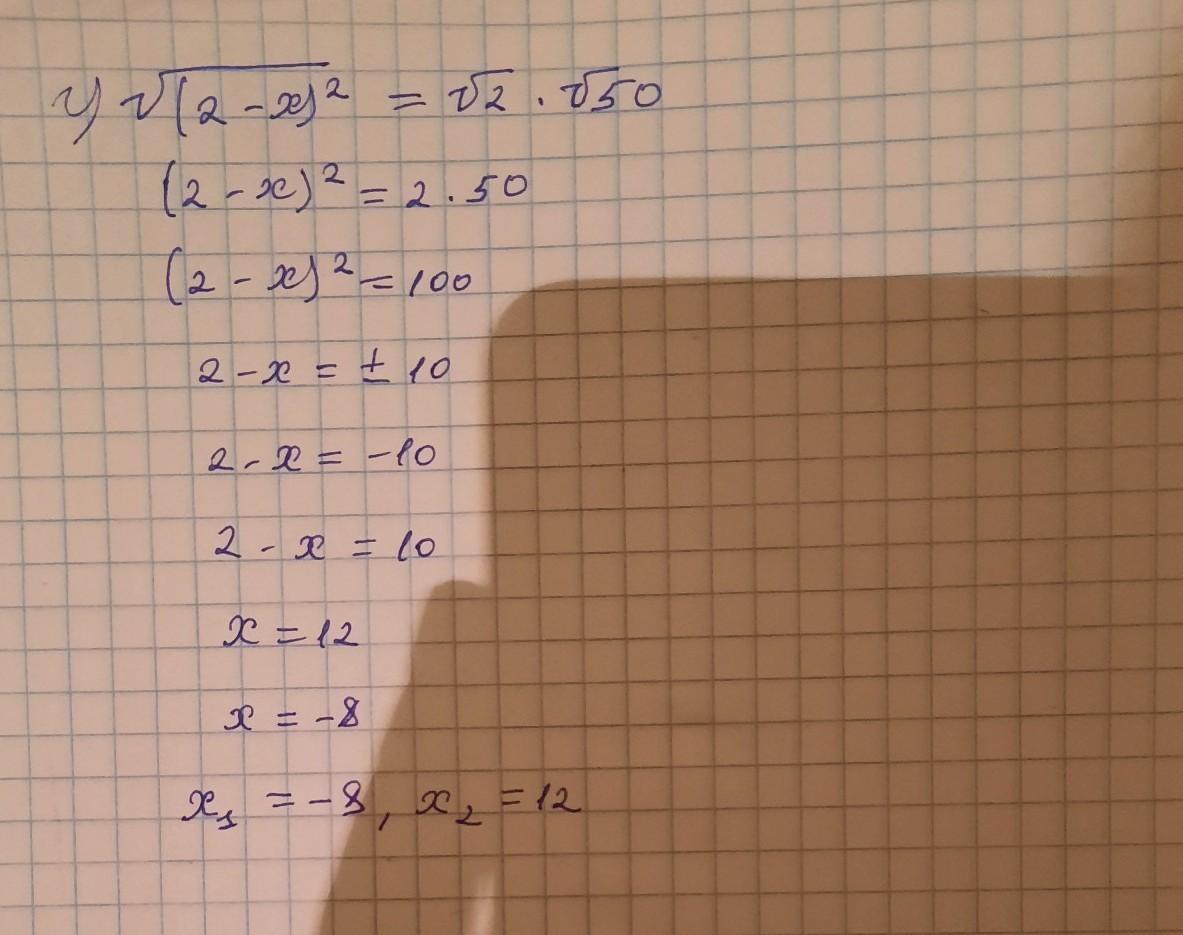
Аноним:
Дрежу)
Похожие вопросы
Предмет: Английский язык,
автор: afrodita8973
Предмет: Русский язык,
автор: 2004nikita2006
Предмет: Английский язык,
автор: eglotova05
Предмет: Математика,
автор: сложик