Предмет: Алгебра,
автор: illtakeyoutohell13
Определите самый большой корень уравнения:
Приложения:
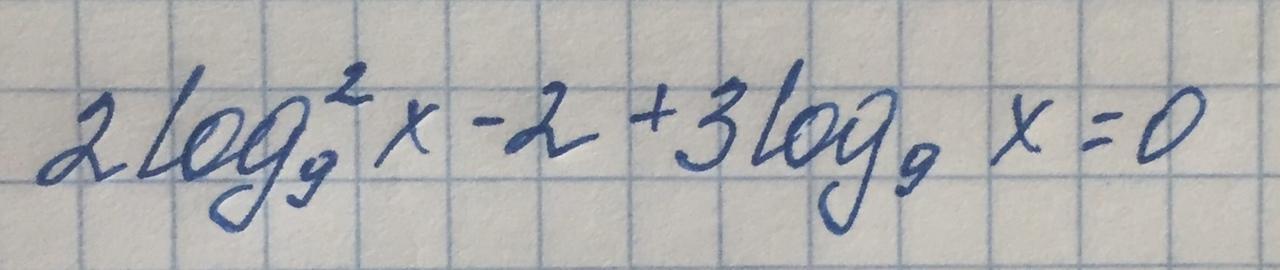
Ответы
Автор ответа:
2
Ответ:
Объяснение:
ОДЗ: x > 0 ⇒ x ∈ (0;+∞)
Замена:
Наибольший x = 3
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: Liza9011
Предмет: Русский язык,
автор: anastasyaaaa1vuabja
Предмет: Биология,
автор: Lkasjdhfg