Question

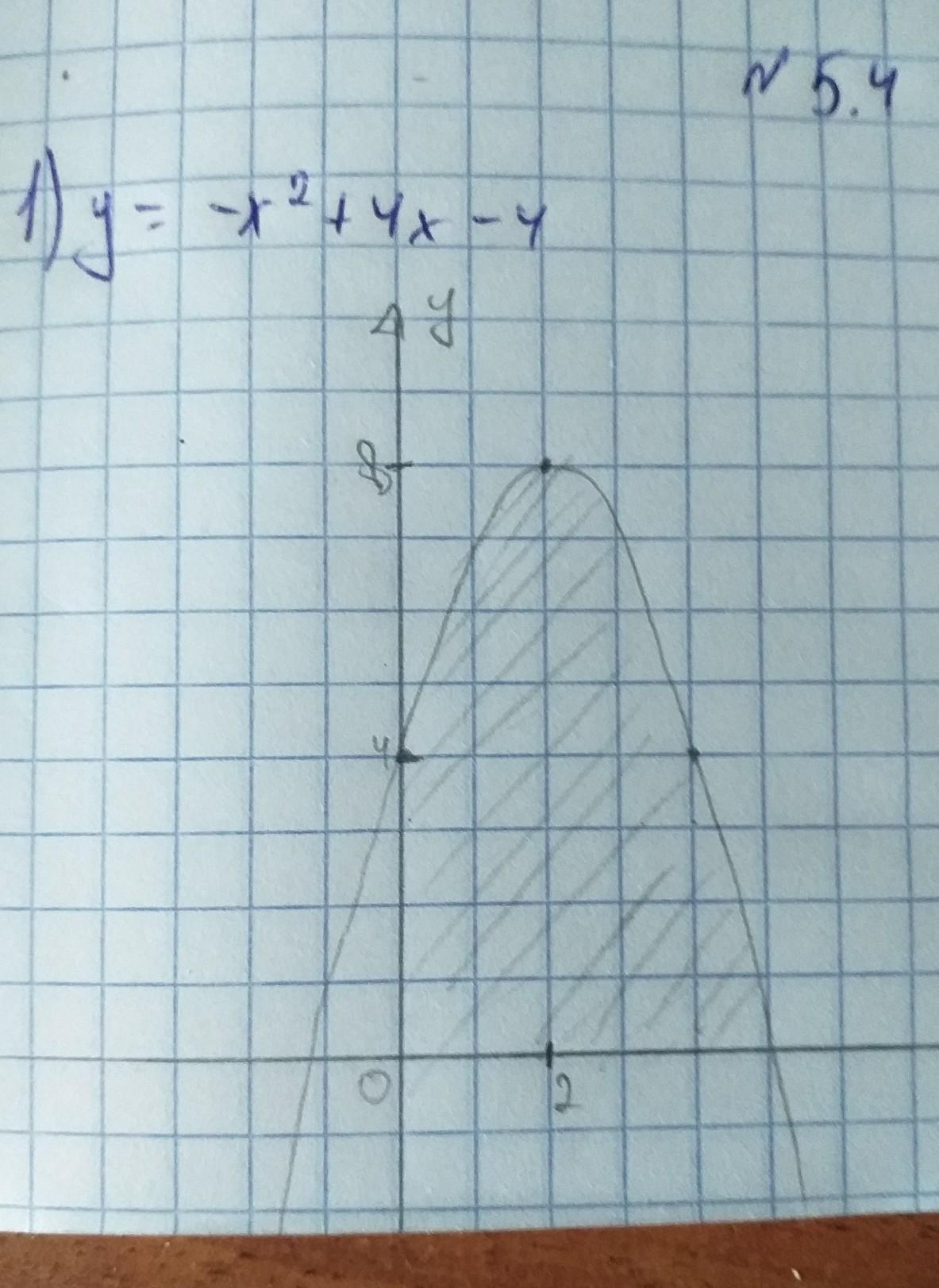
помогите найти площадь фигуры,ограниченной осями координат и параболой
$y = - {x}^{2} + 4x - 4$
​

Answer 1

Ответ:

$\boxed{\dfrac{8}{3}}$ квадратных единиц

Объяснение:

Построим график $y = -x^{2} + 4x - 4$

$y = -(x - 2)^{2}$

$-(x - 2)^{2} \leq 0$ при $x \in \mathbb R$

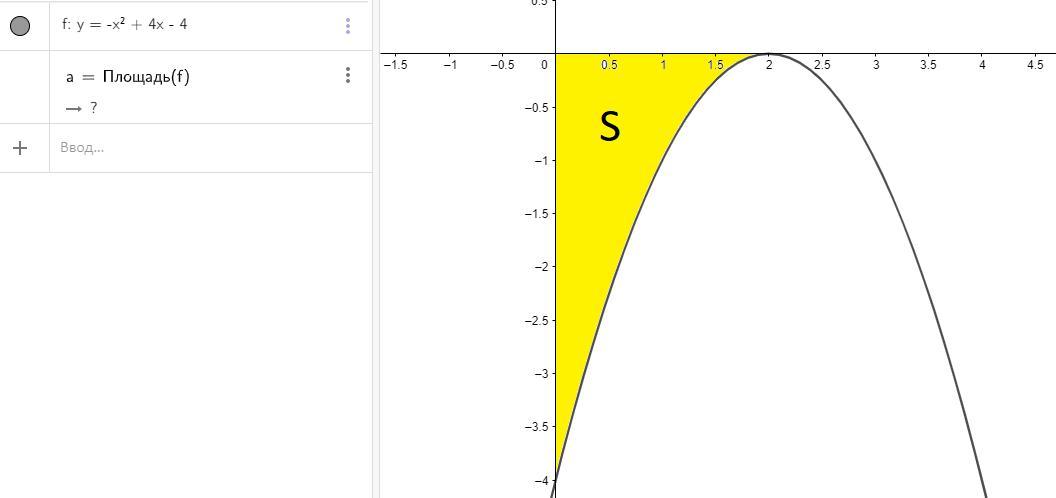
По теореме если функция $f$ непрерывна на отрезке $[b;a]$ и для всех $x \in [b;a]$ выполняется неравенство $f(x) \leq 0$, то $\displaystyle \int\limits^a_b {f(x)} \, dx = -S$, где S - площадь фигуры под графиком, ограниченной линиями x = a, x = b,

y = 0 и графиком функции $f$.

То есть $\displaystyle \int\limits^a_b {-(x - 2)^{2}} \, dx = -S$

$-\displaystyle \int\limits^a_b {(x - 2)^{2}} \, dx = -S |*(-1)$

$S = \displaystyle \int\limits^a_b {(x - 2)^{2}} \, dx$

Найдем точки пересечения графика функции $y = (x- 2)^{2}$ с осями координат.

$y = 0$

$(x - 2)^{2} = 0 \Longrightarrow x - 2 = 0\Longrightarrow x = 2$

$x = 0$

$y(0) = (0 - 2)^{2} = 4$

(0;4), (2;0)

Пределы интегрирования:

a = 2

b = 0

Посчитаем неопределенный интеграл:

$\displaystyle \int {-y} \, dx =\displaystyle \int {(x- 2)^{2}} \, dx= \displaystyle \int {(x^{2} -4x + 4)} \, dx = \displaystyle \int {x^{2}} \, dx - \displaystyle \int {4x} \, dx + \displaystyle \int {4} \, dx =$

$= \displaystyle \int {x^{2}} \, dx - \displaystyle4 \int {x} \, dx + \displaystyle 4\int {1\cdot} \, dx = \dfrac{x^{3}}{3} + C_{1} - \dfrac{4x^{2} }{2} + C_{2} + 4x + C_{3} =$

$=\dfrac{x^{3}}{3} - 2x^{2}+ 4x + C$

$S = \displaystyle \int\limits^a_b {(x - 2)^{2}} \, dx = \displaystyle \int\limits^2_0 {(x - 2)^{2}} \, dx = \dfrac{x^{3}}{3} - 2x^{2}+ 4x \bigg|_0^2 = \dfrac{2^{3}}{3} - 2 \cdot 2^{2}+ 4\cdot 2 -$

$- \left( \dfrac{0^{3}}{3} - 2 \cdot 0^{2}+ 4\cdot 0 \right) = \dfrac{8}{3} - 2 \cdot 4+ 4\cdot 2 = \dfrac{8}{3}$