Предмет: Геометрия,
автор: Zinardo
Дано:
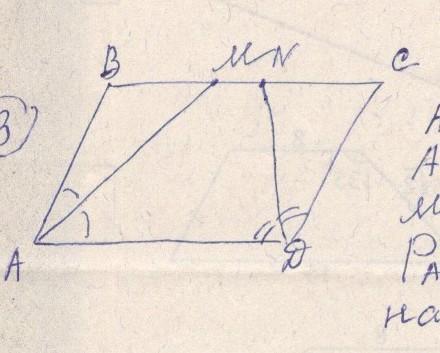
ABCD - параллелограмм
AM и DN - биссектрисы угла BAD и угла ADC
MN = 8см
Периметр ABCD= 46 СМ
Найти стороны параллелограма
Приложения:
Ответы
Автор ответа:
2
Ответ:
АВ = CD = 5см.
ВС = AD = 18 см.
Объяснение:
Биссектрисы углов параллелограмма отсекают от него равнобедренные треугольники (свойство). Следовательно, треугольники АВМ и NCD равнобедренные и в них ВМ = СN и CN = CD соответственно.
Так как противоположные стороны параллелограмма равны, то:
ВМ = СN = AB, DC = AD = 2AB+8 и периметр параллелограмма равен
46 = 2·(AB + AD) = 2·(AB + 2AB+8) = 6·AB +16. =>
АВ = (46-16)/6 = 5 см.
AD = 2АВ +8 = 18 см.
Похожие вопросы
Предмет: Немецкий язык,
автор: ale68
Предмет: Русский язык,
автор: Аноним
Предмет: Українська мова,
автор: katiaostrovets
Предмет: Литература,
автор: parad0x11
Предмет: Математика,
автор: Anastasia2018111