Предмет: Алгебра,
автор: mysticstylez
Помогите решить, на картинке
Приложения:
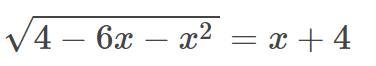
Ответы
Автор ответа:
0
Ответ:
х=-1
Объяснение:
х1= -6, не подходит, т.к.
√4-6•(-6)-(-6)² = -6+4
√4+36-36 = -2
√4 ≠ -2
Похожие вопросы
Предмет: Другие предметы,
автор: magomed1588
Предмет: Русский язык,
автор: ававав3
Предмет: Английский язык,
автор: moyo2
Предмет: Русский язык,
автор: Angelikup
Предмет: Математика,
автор: danilpristupa2