Question

помогите решить срочно Казакова наглядная геометрия 9​

Answer 1

Ответ:

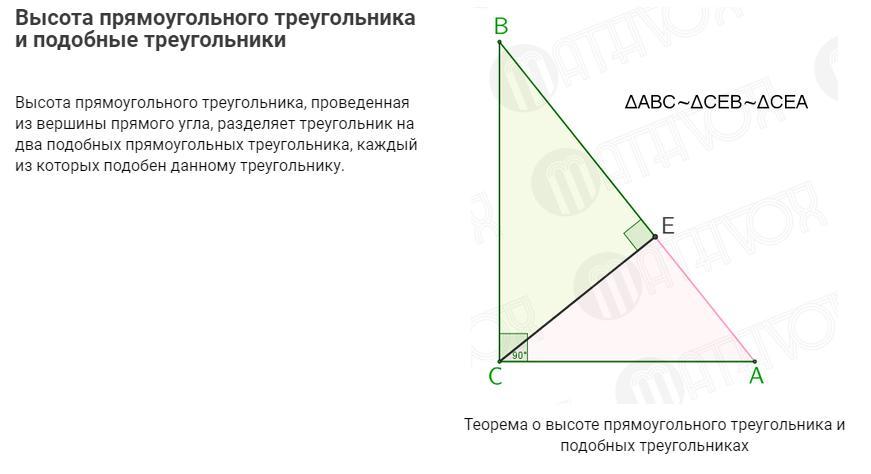
Используя теорему о высоте прямоугольного треугольника, и подобных треугольниках (см. картинку) - полетели:

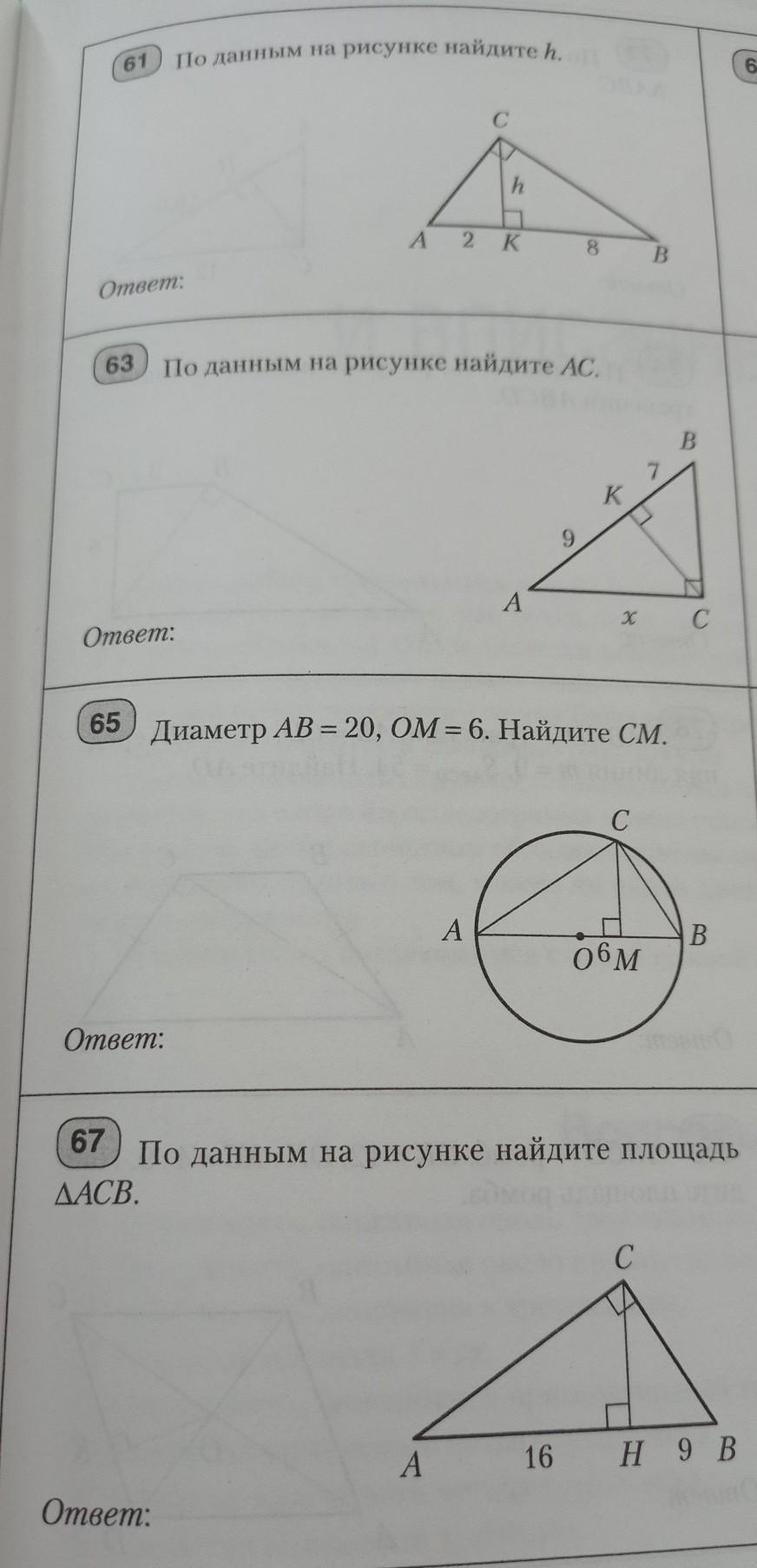
61) Т.к. Δ BKC ≡ Δ CKA ⇒ Их стороны пропорционально равны, а это значит что:

$\frac{KB}{CK} = \frac{CK}{AK}\\\\CK^{2} = KB*AK\\\\CK^{2} = 8*2\\\\CK = \sqrt{16} \\\\CK = h = 4$

63) Т.к. Δ BKC ≡ Δ CKA ⇒ Их стороны пропорционально равны, а это значит что:

$\frac{AK}{KC} = \frac{KC}{KB}\\\\KC^{2} = AK*KB\\\\KC^{2} = 9*7\\\\KC = 3\sqrt{7}$

Далее рассмотрим Δ AKC:

В нём один катет AK = 9. Второй катет KC = 3√7. Остаётся найти гипотенузу AC. Применяем теорему Пифагора:

$AC^{2} = AK^{2} + KC^{2} \\\\AC^{2} = 9^{2} + (3\sqrt{7})^{2} \\\\AC = \sqrt{81 + 63}\\\\AC = \sqrt{144}\\\\AC = 12$

65) Т.к. AO и OB - это радиусы окружности ⇒

$AO = OB = \frac{20}{2} = 10$

Далее:

AM = AO + OM = 10 + 6 = 16

⇒ MB = OB - OM = 10 - 6 = 4

Т.к. Δ ACM ≡ Δ CBM ⇒ Их стороны пропорционально равны, а это значит что:

$\frac{AM}{CM} = \frac{CM}{MB} \\\\CM^{2} = AM*MB\\\\CM^{2} = 16*4\\\\CM = \sqrt{64}\\\\CM = 8$

67) Т.к. Δ ACH ≡ Δ CBH ⇒ Их стороны пропорционально равны, а это значит что:

$\frac{AH}{CH} = \frac{CH}{HB} \\\\CH^{2} = AH*HB\\\\CH^{2} = 16*9\\\\CH = \sqrt{144}\\\\CH = 12$

Далее: Рассмотрим Δ ACB

Применяем формулу площади прямоугольного треугольника через высоту, проведённую к его основанию:

$S = \frac{1}{2}* CH*AB\\\\S = \frac{12*(16+9)}{2}\\\\S = 6*25\\\\S = 150$