Предмет: Алгебра,
автор: Kkiiiiiigggiii
помогите пожалуйста, ничего не понимаю
Приложения:
Ответы
Автор ответа:
0
Объяснение:
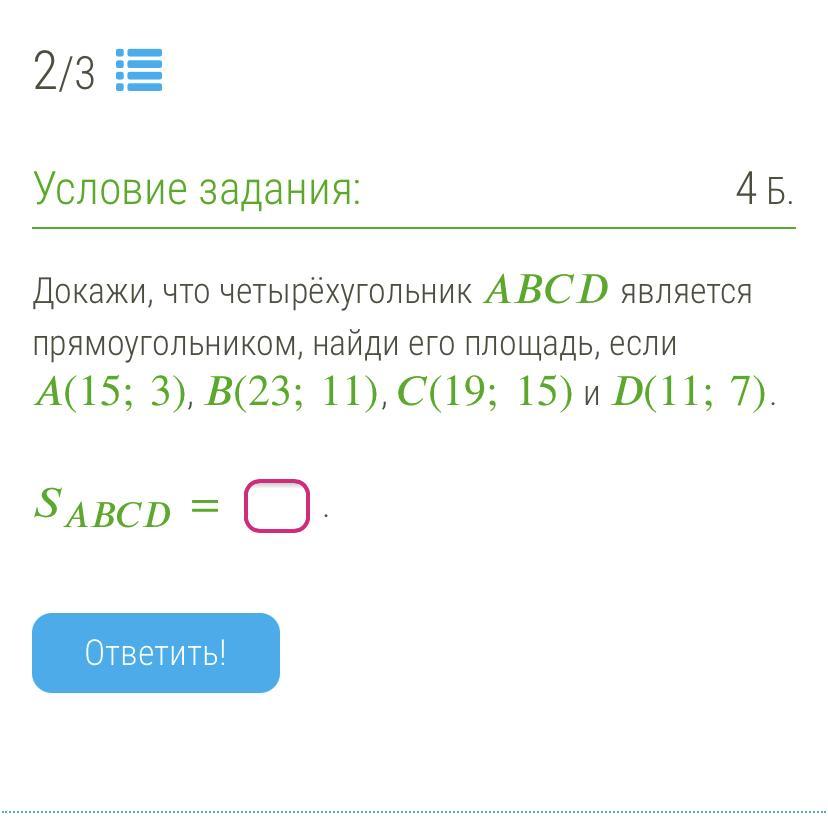
Четырёхугольник АВСD; А(15;3), B(23;11), C(19;15), D(11;7).
Вычислим длины сторон четырёхугольника:
Ответ:
Похожие вопросы
Предмет: Українська мова,
автор: н6н
Предмет: Другие предметы,
автор: юбка
Предмет: Русский язык,
автор: lidakardanova93
Предмет: История,
автор: kiraplayg40
Предмет: Алгебра,
автор: maxik495