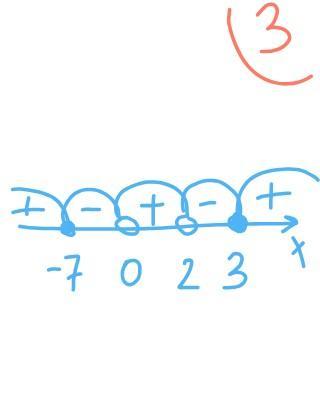Question

Помогите решить неравенство

Answer 1

Решаю методом интервалов.

Приравниваем выражение к нулю, составляем уравнение, находим корни уравнения и обозначаем их точками на прямой. В интервалах между точками проставляем знаки и выбираем нужные интервалы — они будут решением неравенства.

Итак, первое неравенство:

$(x - 2)(x + 6)(x - 4) > 0$

Приравниваем выражение к нулю.

$(x - 2)(x + 6)(x - 4) = 0$

$x_1 = 2, x_2 = - 6, x_3 = 4$

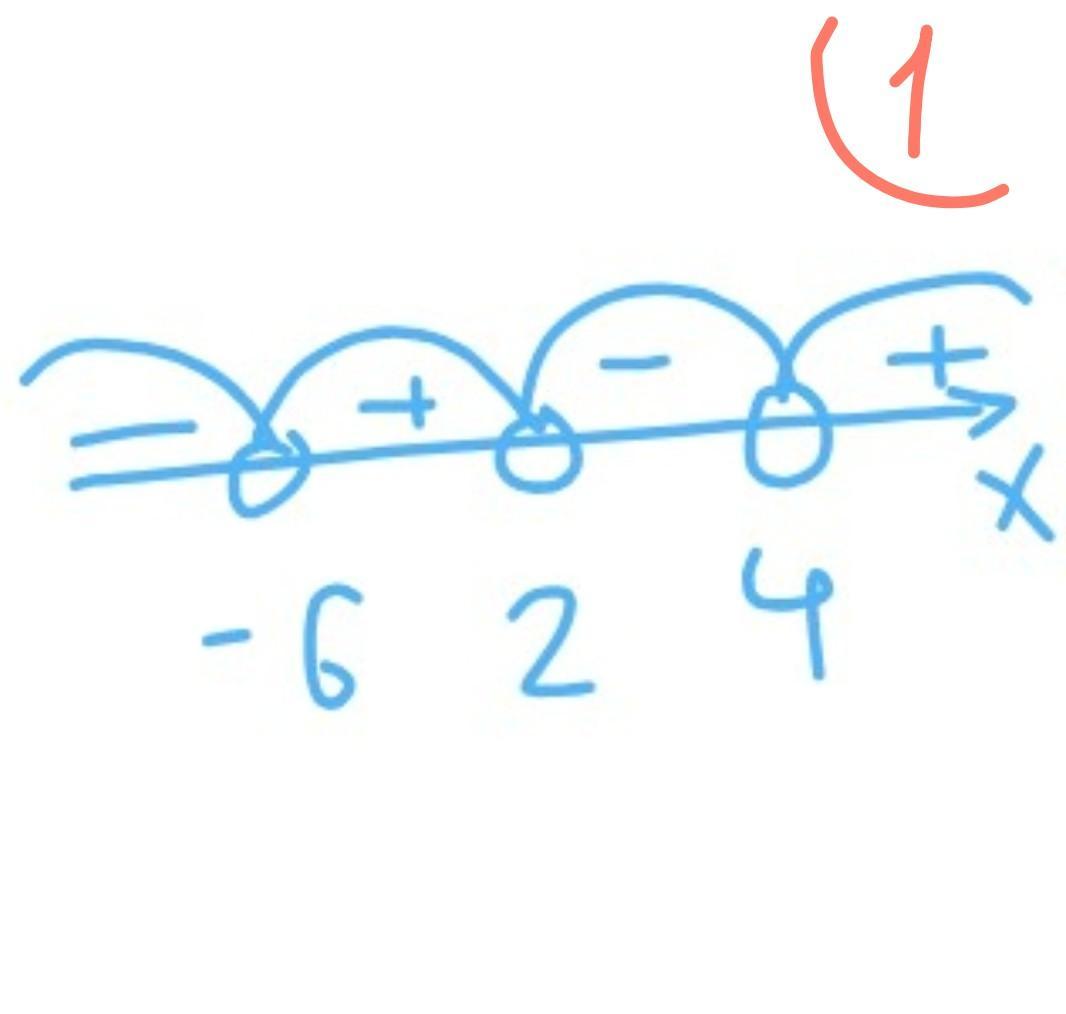
Обозначаем эти точки на прямой. Знак неравенства строгий (только больше), значит точки незакрашенные. <рисунок1>. Расставляем знаки в интервалах. Берём любое число, принадлежащее интервалу (но не сами точки), подставляем в исходное выражение и смотрим на решение, если в ответе будет положительное число, ставим «+», если отрицательное — «–». Например, первый интервал до -6, возьмём -7. (-7-2)(-7+6)(-7-4)=(-9)×(-1)×(-11)=(-99) — знак «–», второй интервал от -6 до 2, возьмём 0. (0-2)(0+6)(0-4)=(-2)×6×(-4)=48 — знак «+». Третий интервал от 2 до 4, берём 3. (3-2)(3+6)(3-4)=1×9×(-1)=(-9) — знак «–». И последний интервал от 4 до бесконечности, возьмём 5. (5-2)(5+6)(5-4)=3×11×1=33 — знак «+».

Теперь вспоминаем какой знак у нашего неравенства — "больше", значит интервалы со знаком «+» будут решением неравенства.

Если точки незакрашенные, то скобки круглые, если точки закрашенные, то скобки квадратные. Вот и все хитрости. :)

Ответ: $x \in(-6;2) \cup (4; + \infty )$

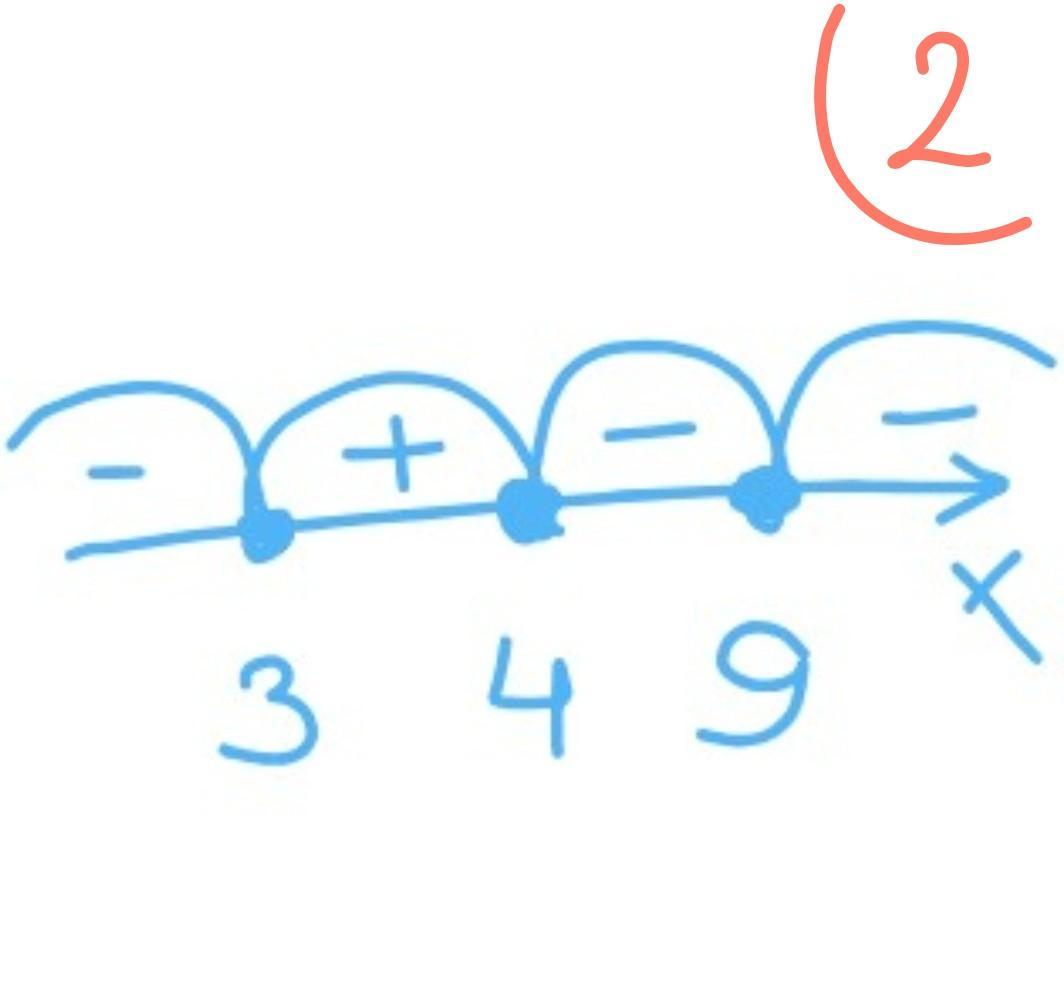
Второе неравенство:

$(3 - x)(x - 4) {(x - 9)}^{2} \geqslant 0$

$(3 - x)(x - 4) {(x - 9)}^{2} = 0$

$3-x=0, \: x_1 = 3;$

$x - 4 = 0, \: x_2 = 4;$

${(x - 9)}^{2} = 0, \: x-9=0, \: x_3=9$

<рисунок2>

${(x - 9)}^{2}$ при x = 9 равно 0, а значит и значение всего выражения $(3 - x)(x - 4) {(x - 9)}^{2}$ равно 0, что удовлетворяет условию неравенства (меньше или равно нулю), число 9 тоже является решением неравенства.

Ответ: $x \in[3; 4] \cup [9]$

Третье неравенство:

$\frac{x}{x - 2} + \frac{4}{x} - \frac{13}{ {x}^{2} - 2x} \leqslant 0$

Здесь в знаменателе появилась переменная x, это неравенство дробное рациональное. Решим так же, методом интервалов.

Приведём дроби к общему знаменателю.

$\frac{x \times x}{(x - 2) \times x} + \frac{4 \times (x - 2)}{x \times (x - 2)} - \frac{13}{ {x}^{2} - 2x} \leqslant 0$

$\frac{ {x}^{2} }{ {x}^{2} - 2x } + \frac{4x - 8}{ {x}^{2} - 2x} - \frac{13}{ {x}^{2} - 2x} \leqslant 0$

$\frac{ {x}^{2} + 4x - 8 - 13}{ {x}^{2} - 2x} \leqslant 0$

$\frac{ {x}^{2} + 4x - 21}{ {x}^{2} - 2x } \leqslant 0$

Сначала найдем нули знаменателя. Приравняем знаменатель к нулю, найдём точки-"исключения".

${x}^{2} - 2x = 0$

$x(x - 2) = 0$

$x_1=0; \: \: x-2=0, \: x_2 = 2$

Нули знаменателя всегда отмечаются на прямой как незакрашенные точки.

Теперь найдём нули числителя. Приравниваем числитель к нулю.

${x}^{2} + 4x - 21 = 0$

$D = {b}^{2} - 4ac = {4}^{2} - 4 \times 1 \times ( - 21) = 16 + 84 = 100 = {10}^{2}$

$x_1 = \frac{ - b + \sqrt{D} }{2a} = \frac{ - 4 + 10}{2} = \frac{6}{2} = 3$

$x_2 = \frac{ - b - \sqrt{D} }{2a} = \frac{ - 4 - 10}{2} = \frac{ - 14}{2} = - 7$

Знак нашего неравенства нестрогий (меньше или равно), нули числителя отмечаем на прямой как закрашенные точки.

<рисунок3>

Ответ: $x \in [- 7; 0) \cup (2; 3]$