Предмет: Математика,
автор: sasasihov65
Решите всё задание даю 50 баллов
Приложения:
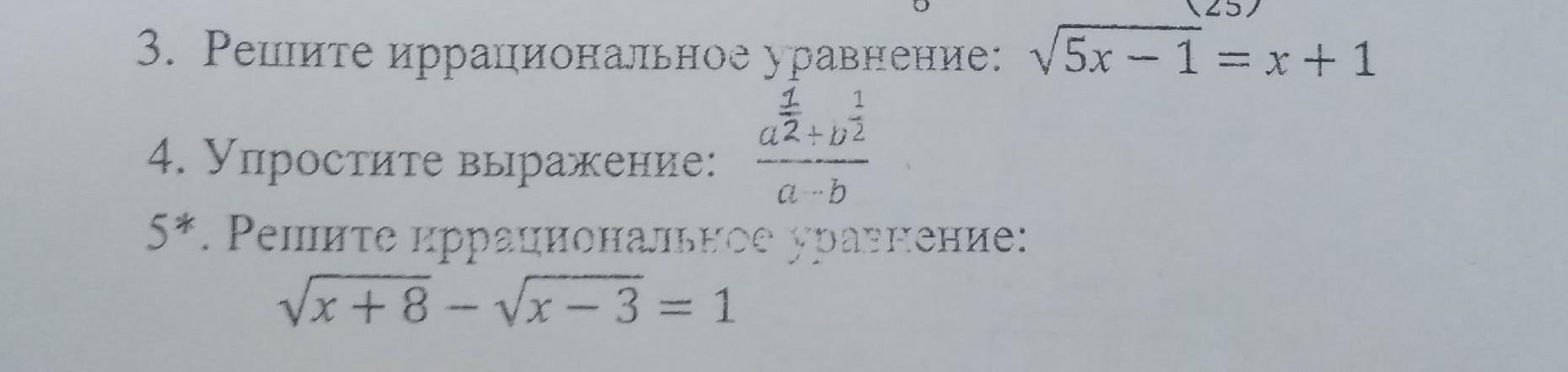
Ответы
Автор ответа:
2
3.
Опередим область определения функции:
D(y): 5x - 1 ≥ 0
5x ≥ 1
x ≥ 0,2
D(y) = [0,2; +∞)
x² - 3x + 2 = 0
D = (-3)² - 4 • 2 = 1
Ответ: 1; 2
4.
5.
Определим область определения функции:
D(y): x + 8 ≥ 0 и x - 3 ≥ 0
x ≥ -8 и x ≥ 3
D(y) = [3; +∞)
Область определения функции — это значения аргумента (x), при которых функция (y) будет иметь смысл
Похожие вопросы
Предмет: Технология,
автор: Moon1231
Предмет: Русский язык,
автор: nastya200107
Предмет: Русский язык,
автор: iri12sha
Предмет: Математика,
автор: Афатима2007
Предмет: География,
автор: darkwood77