Question

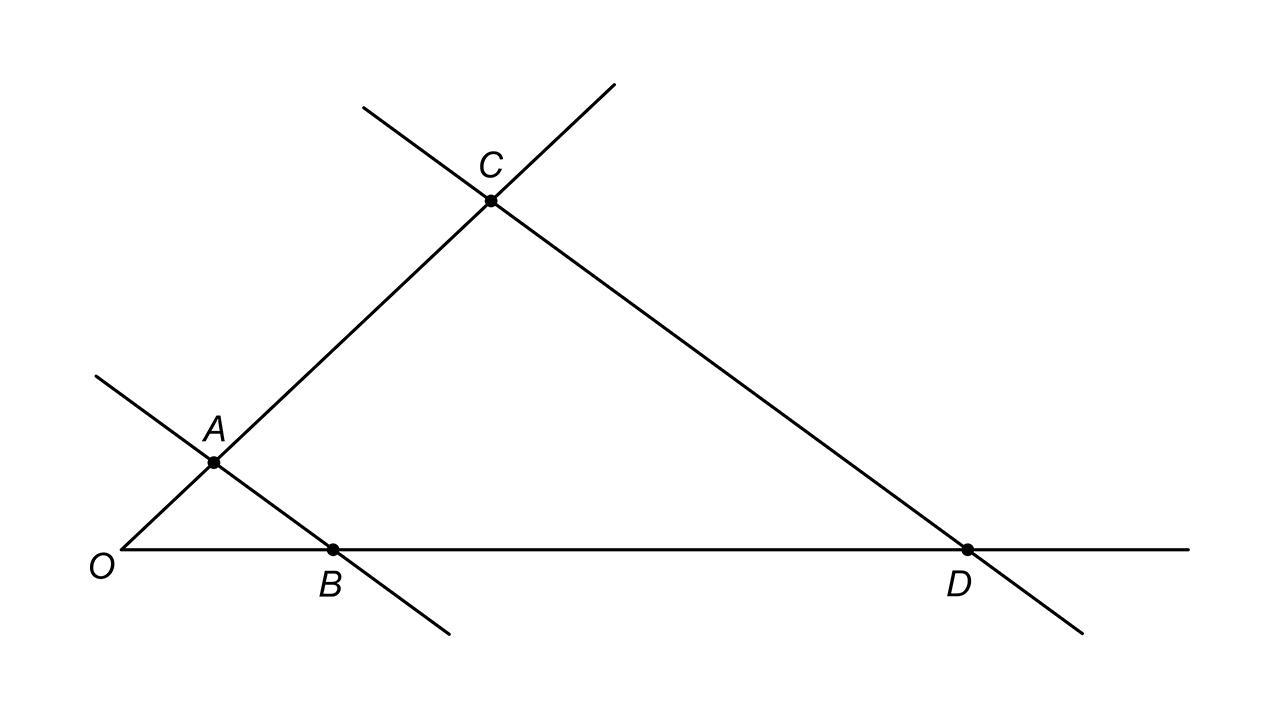
стороны угла с вершиной o пересечены двумя параллельными прямыми в точках a, b и c, d соответственно. найдите oc и od, если oa:ob=3,5 и od-oc=8см​

Answer 1

Ответ:

OC = 12 см

OD = 20 см

Объяснение:

Так как линии параллельны ⇒ Δ OAB ≡ Δ OCD ⇒ OA пропорциональна OC, и OB пропорциональна OD ⇒

$\frac{OA}{OB} = \frac{OC}{OD} = \frac{3}{5}$

Составляем систему уравнений:

$\left \{ {{\frac{OC}{OD} = \frac{3}{5}} \atop {OD-OC=8}} \right.$

Найдём чему равно OС из первого уравнения:

$OC = \frac{3*OD}{5}$

Подставим полученное значение OC во второе уравнение, и найдём чему равно OD:

$OD - \frac{3*OD}{5} = 8\\\\5*OD - 3*OD = 40\\\\2*OD = 40\\\\OD = \frac{40}{2}\\\\OD = 20 cm$

Подставим полученное значение OD в первое уравнение, и найдём чему равно OC:

$\frac{OC}{20} = \frac{3}{5}}\\\\OC = \frac{20*3}{5}\\\\OC = 4*3\\\\OC = 12 cm$