Question

ВЫСШАЯ МАТЕМАТИКА!
ПРИМЕР ВО ВЛОЖЕНИИ.
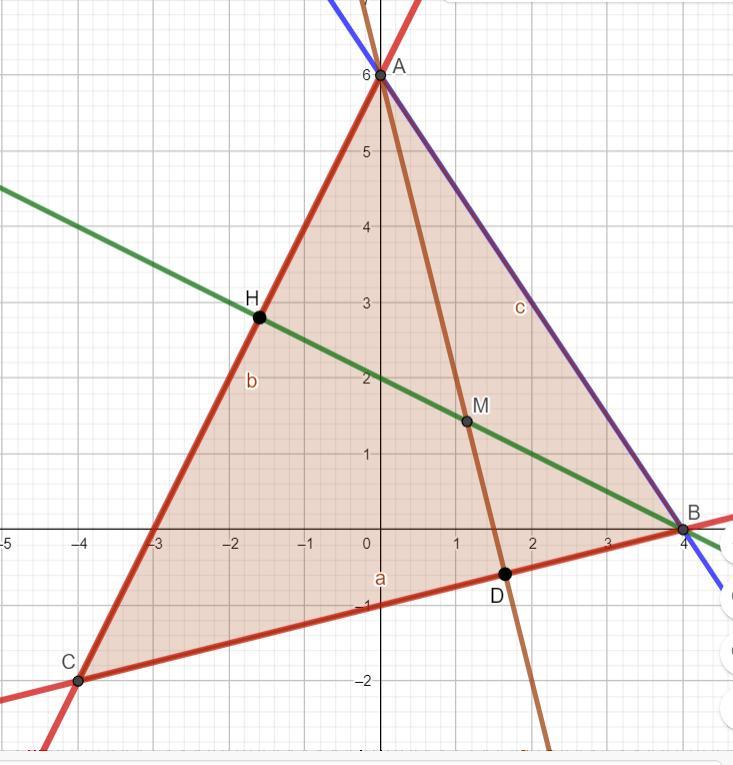
Написать уравнения сторон AC и BC .

Answer 1

Пересечение стороны АВ с высотами АМ и ВМ даёт координаты точек А и В. Определяем точку А.

3x + 2y = 12

4x + y = 6 умножим на минус 2.

3x + 2y = 12

-8x - 2y = -12  

-5x        = 0,

x = 0, y = 6 - 4x = 6 - 4*0 = 6.

Точка А(0; 6).

Определяем точку В.

3x + 2y = 12

x + 2y = 4 вычтем из первого уравнения второе

2x       = 8

x = 8/2 = 4, y = (4 - x)/2 = (4 - 4)/2 = 0.

Точка В(4; 0).

Переходим к стороне АС.

Она перпендикулярна высоте ВМ. В уравнении перпендикуляра меняются коэффициенты: В становится А, а А становится -В.

ВМ: x + 2y - 4 = 0,

AC: 2x - y + C = 0. Для определения  слагаемого С подставим координаты точки А:

АС: 2*0 - 6 + С = 0. Отсюда С = 6.

Уравнение АС: 2x - y + 6 = 0.

Переходим к стороне BС.

Она перпендикулярна высоте АМ. В уравнении перпендикуляра меняются коэффициенты: В становится А, а А становится -В.

АМ:4x + y - 6 = 0,

ВC: x - 4y + C = 0. Для определения  слагаемого С подставим координаты точки В:

ВС: 4 - 4*0 + С = 0. Отсюда С = -4.

Уравнение ВС: x - 4y - 4 = 0.