Question

сроячно пж, с полным разбором!!!!!!​

Answer 1

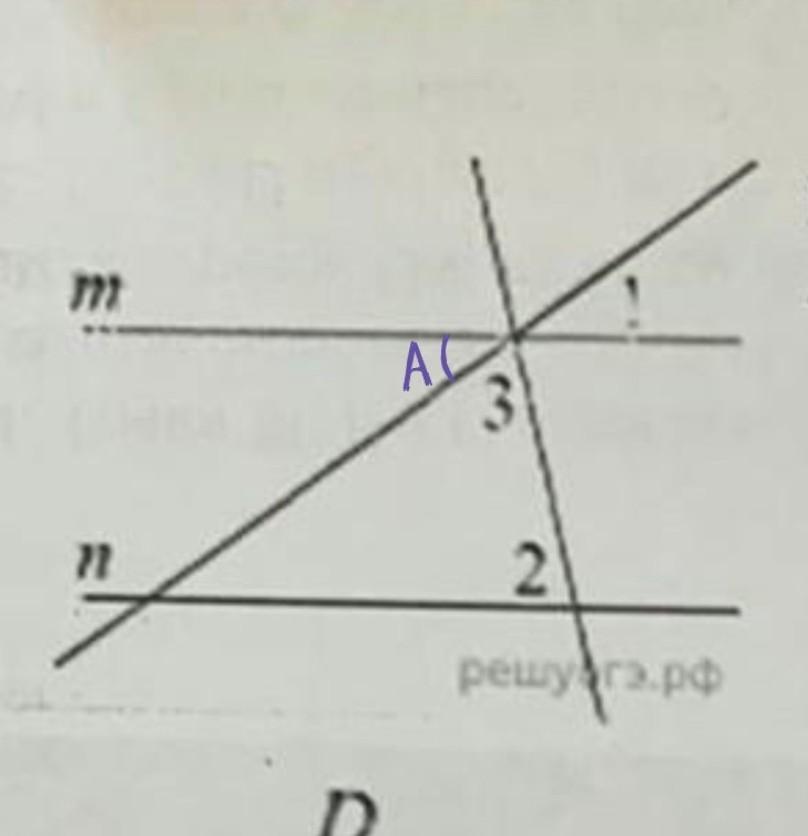
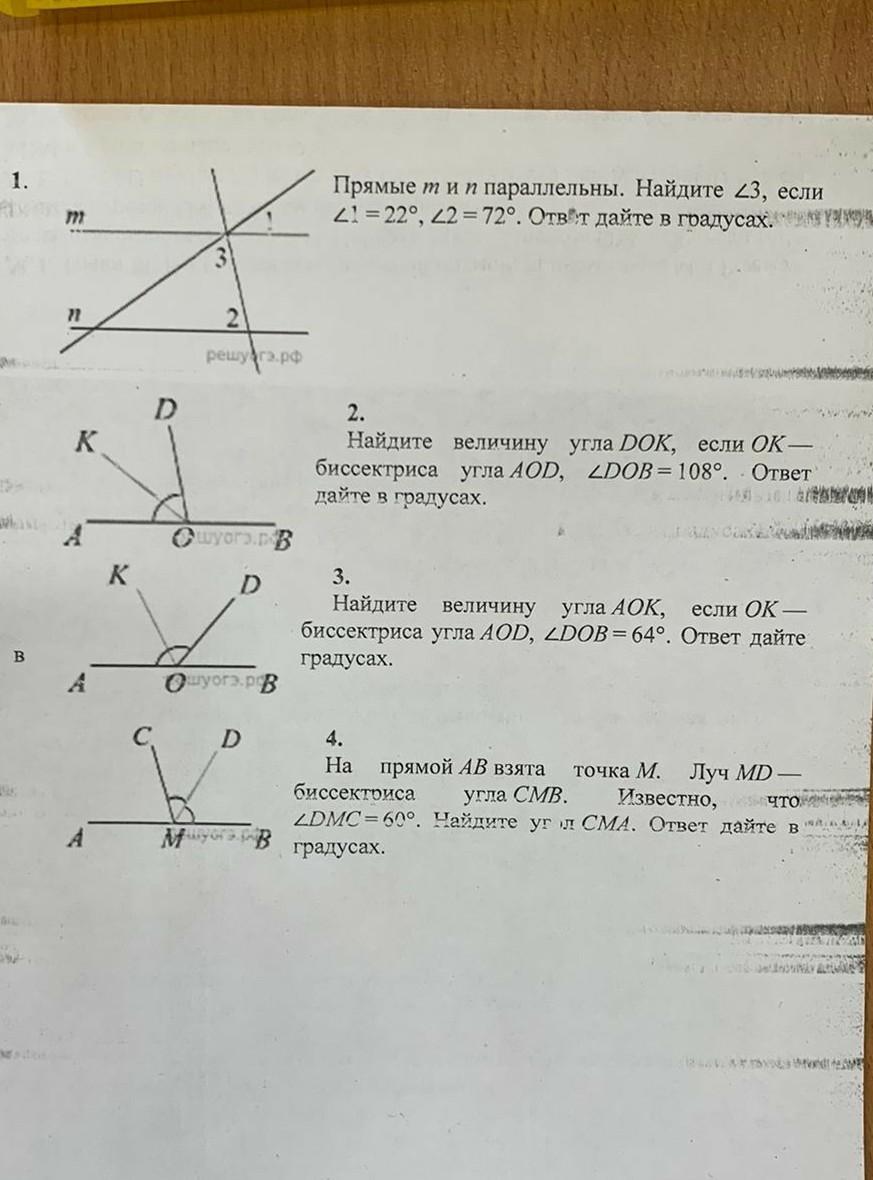
Рисунок 1. ∡А и ∡1 — вертикальные углы (стороны одного угла являются продолжениями сторон другого угла), а вертикальные углы равны => ∡А = ∡1 = 22°.

(∡А+∡3) и ∡2 — внутренние односторонние углы (по свойству секущей двух параллельных прямых, m || n), внутренние односторонние углы в сумме составляют 180° => ∡А + ∡3 + ∡2 = 180°, ∡3 = 180° – ∡А – ∡2 = 180° – 22° – 72° = 86°.

Ответ: ∡3 = 86°

Рисунок 2. ∡AOB — развёрнутый угол, ∡AOB = 180°. ∡AOB = ∡AOD + ∡DOB, ∡AOD = ∡AOB – ∡DOB = 180° – 108° = 72°.

OK — биссектрисса ∡AOD, делит его на два равных угла => ∡AOK = ∡DOK = 1/2 × ∡AOD = 1/2 × 72° = 36°.

Ответ: ∡DOK = 36°

Рисунок 3. Эта задача аналогична задаче 2.

∡AOB — развёрнутый угол, ∡AOB = 180°. ∡AOB = ∡AOD + ∡DOB, ∡AOD = ∡AOB – ∡DOB = 180° – 64° = 116°.

OK — биссектрисса ∡AOD, делит его на два равных угла => ∡AOK = ∡DOK = 1/2 × ∡AOD = 1/2 × 116° = 58°.

Ответ: ∡AOK = 58°

Рисунок 4. Тоже аналогичная задача.

∡AOM — развёрнутый угол, ∡AMB = 180°.

∡AMB = ∡CMA + ∡CMB, ∡CMA = ∡AMB – ∡CMB.

MD — биссектрисса ∡CMB, делит его на два равных угла => ∡DMC = ∡DMB = 1/2 × ∡CMB, ∡CMB = 2 × ∡DMC = 2 × 60° = 120°.

∡CMA = ∡AMB – ∡CMB = 180° – 120° = 60°

Ответ: ∡CMA = 60°