Предмет: Алгебра,
автор: nikita4222
найти область определения функции
Приложения:
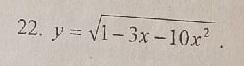
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Т. к. подкоренное выражение должно быть больше 0 или равно 0, то
Автор ответа:
0
Обл.определения функции: у=0, решаем уравнение 1-3х-10х²=0
10x²+3x-1=0
10x²+5x-2x-1=0
5x(2x+1)-(2x+1)=0
(5x-1)(2x+1)=0
5x-1=0 2x+1=0
x=1/5 = 0,2 x=-1/2 = -0,5
тогда х€[-1/2,1/5] или х€[-0,5;02]
Решено верно !!!
Похожие вопросы
Предмет: Технология,
автор: александра4647
Предмет: Русский язык,
автор: ЯрославРаев
Предмет: Русский язык,
автор: kaeserCSGO
Предмет: Русский язык,
автор: маруся520
Предмет: Математика,
автор: chaynick228