Question

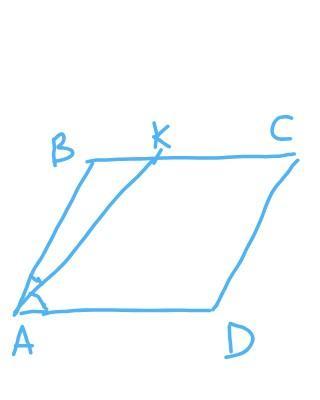
68. Бісектриса кута А паралелограма ABCD ділить сторо-
ну ВС на два відрізки ВК і КС так, що ВК : КС = 3:7.
Знайдіть сторони паралелограма, якщо його периметр
дорівнює 78 см.​

Answer 1

Противоположные стороны параллелограмма равны (свойство параллелограмма) => AB = CD, BC = AD,

Периметр равен сумме всех сторон, поскольку противоположные стороны равны, то периметр равен удвоенной сумме смежных сторон => P = 2(AB+BC) = 78см, 2(AB+BC) = 78см, AB+BC = 39см.

BK:KC = 3:7, BK = 3x, KC = 7x, BK + KC = 3x + 7x = 10x = BC.

Биссектрисса параллелограмма отсекает от него равнобедренный треугольник (свойство параллелограмма) => треуг. ABK — равнобедренный, AB = BK. =>

AB = BK = 3x,

AB + BC = 3x + 10x = 13x = 39см, x = 3см.

AB = 3x = 3 × 3см = 9см,

BC = 10x = 10 × 3см = 30см.

Ответ: AB = 9см, BC = 30см, CD = 9см, AD = 30см.