Предмет: Алгебра,
автор: Аноним
Решить систему линейных уравнений методом Крамера
Приложения:
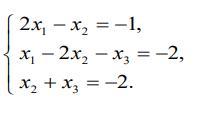
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: i3rkOtigerjgo
Предмет: Английский язык,
автор: syuzi20071
Предмет: Українська література,
автор: kat0002
Предмет: Физика,
автор: Инна111111111112
https://znanija.com/task/45629204