Предмет: Геометрия,
автор: ata221
Основанием треугольной пирамиды является правильный треугольник и все её боковые рёбра равны 15 см, а её высота 12 см. Найдите сторону основания
Приложения:

Ответы
Автор ответа:
3
Ответ:
см
Объяснение:
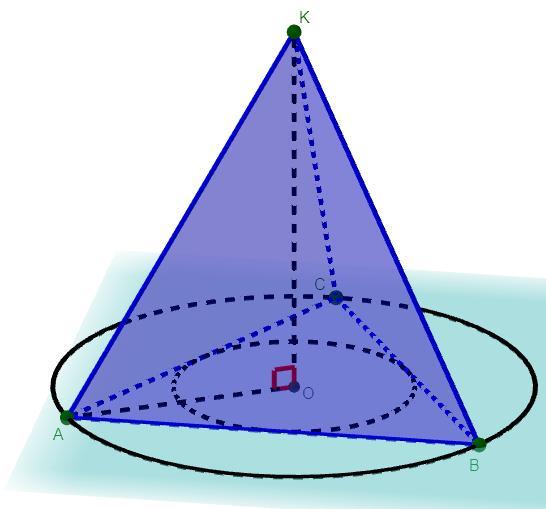
Дано: ABCK - пирамида, AC = AB = BC, KA = KB = KC = 15 см, KO ⊥ ABC,
KO = 12 см
Найти: AC, AB, BC - ?
Решение: Так как по условию основание пирамиды правильный треугольник и KA = KB = KC, то по теореме ABCK - правильная пирамида, тогда точка O центр вписанной окружности треугольника ΔABC.
Проведем отрезок AO. Так как KO ⊥ ABC и AO ⊂ ABC, то KO ⊥ AO. Рассмотрим треугольник AOK. По теореме Пифагора: см. По свойствам правильного треугольника (ΔABC) центр вписанной и описанной окружности треугольника совпадают, тогда AO - радиус описанной окружности. По свойствам правильного треугольника все его углы равны 60°. По следствию из теоремы синусов:
см.
см.
Приложения:
Simba2017:
как можно такие решения давать без чертежа?
Чертеж есть.
Попробуйте обновить страницу
Кстати, с решением все нормально?
теперь вижу
ну я написала ответ в комментариях в одну строку автору)))))
Похожие вопросы
Предмет: Другие предметы,
автор: кир123
Предмет: Русский язык,
автор: 18062
Предмет: Русский язык,
автор: Leoчто
Предмет: Геометрия,
автор: Nikolai15Nikolaevich