Предмет: Алгебра,
автор: abzalovtimur04
Помогите решить, пожалуйста, СРОЧНО
Приложения:
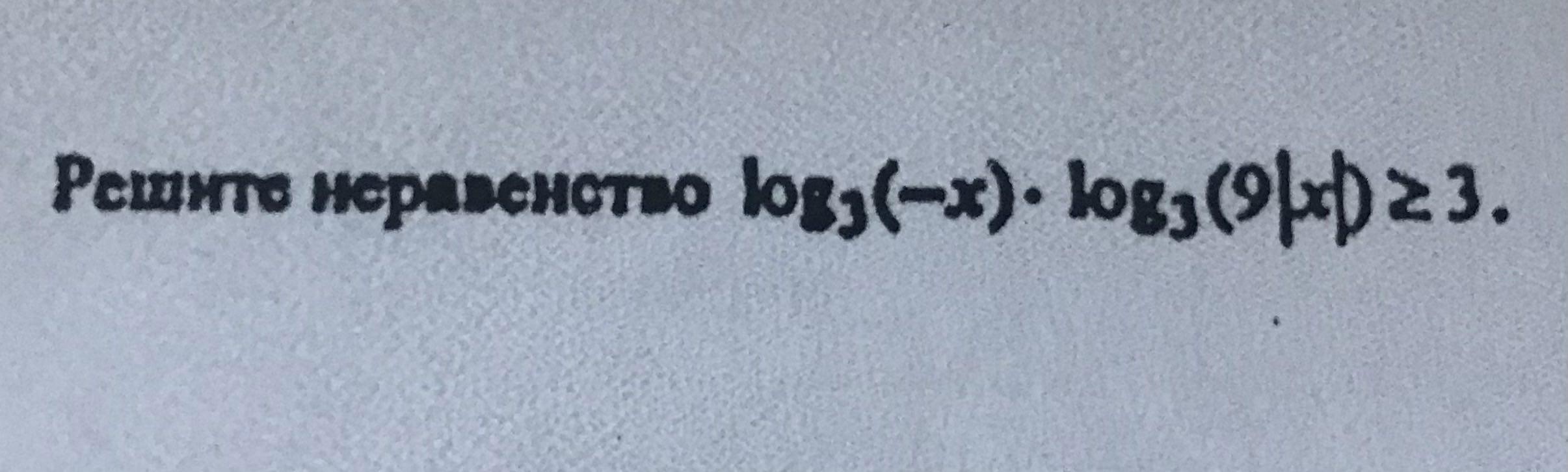
Ответы
Автор ответа:
1
Ответ:
NNNLLL54:
см
Похожие вопросы
Предмет: Русский язык,
автор: рррп1
Предмет: Русский язык,
автор: AlexPomanov
Предмет: Русский язык,
автор: AnzhelikaS14
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: чимини1