Помогите 50 баллов даю срочно!!
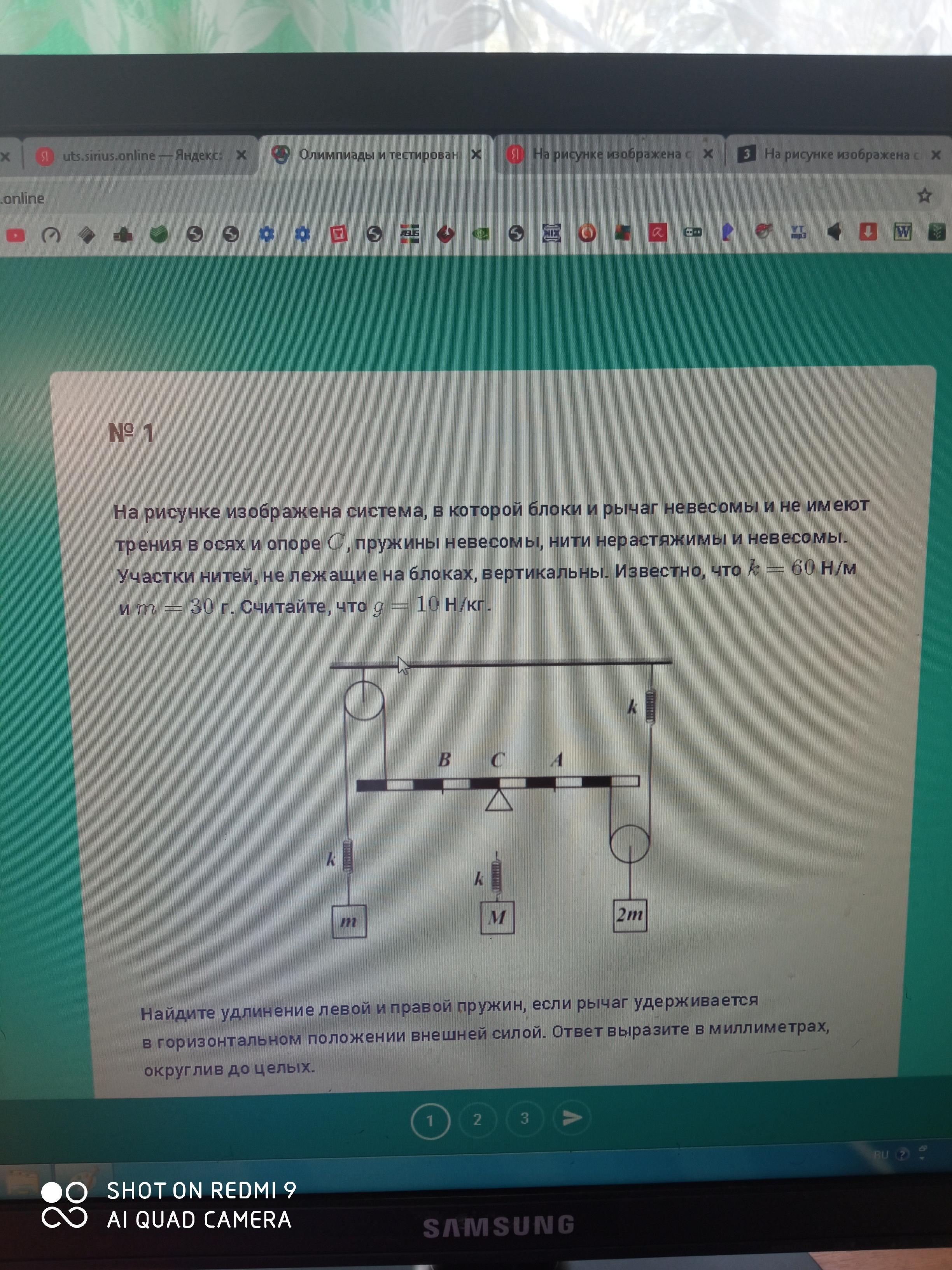
На рисунке изображена система,в которой блоки и рычаг невесомы и не имеют трения в осях и опоре С,пружины невесомы,нити нерастяжимы и невесомы. Участки нитей,не лежащие на блоках,вертикальны.Известно,что k=60H/m и m=30г.Считайте,что g=10H/кг.
Ответы
Дано:
k = 60 Н/м
m = 30 г = 0,03 кг
g = 10 Н/кг
ΔL1, ΔL2, M - ?
Решение:
На рычаг действует внешняя сила F.
На левый груз массой m действует сила тяжести mg. По Третьему закону Ньютона пружина действует на груз силой упругости Fупр1, равной по модулю силе тяжести. С такой же силой пружина действует и на нить, которая через неподвижный блок действует силой натяжения Т1 на рычаг. То есть, на левую часть рычага действует сила натяжения, равная по модулю силе упругости:
Fупр1 = mg
T1 = Fупр1
Примем расстояние от концов рычага до точки опоры С за L. Тогда плечо силы натяжения T1 равно (4/5)*L. Тогда момент силы равен:
М1 = Т1*(4/5)*L = Fупр1*(4/5)*L
На правый груз массой 2m действует сила тяжести 2mg. Через нить эта сила передаётся подвижному блоку. С другой стороны на левую и правую стороны блока действуют две силы, уравновешивающие силу тяжести - силы натяжения нити Т2, которые равны друг другу. Относительно точки опоры подвижного блока, которая находится на рычаге, плечо силы тяжести 2mg в 2 раза меньше, чем плечо силы натяжения Т2. Но сумма моментов этих сил должна равняться нулю, т.к. рычаг находится в равновесии. Значит, сила натяжения Т2 в 2 раза меньше силы тяжести 2mg. Следовательно, на правую сторону рычага действует сила mg.
Сила Т2 по модулю равна силе упругости Fупр2, действующей со стороны пружины на нить. Плечо силы Т2 равно (4/5)*L. Значит, момент силы на правую сторону рычага можно записать так:
Т2 = 2mg/2 = mg
М2 = Т2*(4/5)*L = Fупр2*(4/5)*L
Моменты М1 и М2 стремятся вращать тело по часовой. Но благодаря внешней силе рычаг находится в равновесии. Эту внешнюю силу можно заменить силой тяжести, которая действует на груз массой М, если его подвесить в точке В. Плечо силы равно (2/5)*L. На сам рычаг будет действовать сила упругости пружины, которая равна по модулю силе тяжести Mg. Тогда уравнение моментов будет таким:
Mg = Fупр3
Fупр3*(2/5)*L - Fупр1*(4/5)*L - Fупр2*(4/5)*L = 0
Сразу ответим на вопрос об изменении длин левой и правой пружин. Т.к. T1 = mg и T2 = mg, а Fупр1 = Т1, Fупр2 = Т2, то
Fупр1 = Fупр2 = mg
Fупр = k*ΔL =>
=> k*ΔL = mg
ΔL = ΔL1 = ΔL2 = mg/k = 0,03*10/60 = 0,005 м = 5 мм
Теперь выясним массу груза М и изменение длины его пружины:
Fупр3*(2/5)*L - Fупр1*(4/5)*L - Fупр2*(4/5)*L = 0
Fупр3*(2/5)*L = Fупр1*(4/5)*L + Fупр2*(4/5)*L
Fупр3*(2/5)*L = 2*Fупр*(4/5)*L | * (5/L)
2*Fупр3 = 8*Fупр
2*Mg = 8*mg | : g
2M = 8m
M = 4m = 4*0,03 = 0,12 кг = 120 г
Fупр3 = Mg
k*ΔL3 = Mg
ΔL3 = Mg/k = 0,12*10/60 = 0,02 м = 20 мм
Ответ: 5 мм; 120 г; 20 мм.