Предмет: Алгебра,
автор: Аноним
Решить систему линейных уравнений методом Крамера
Приложения:
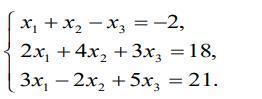
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Английский язык,
автор: ева4160
Предмет: Английский язык,
автор: zhanok96
Предмет: Українська мова,
автор: mkorolishin
Предмет: Математика,
автор: sisi4ki1