Question

Из точки вне прямой проведены к этой прямой две наклонные и перпендикуляр. Сумма наклонных равна 56 см, а их проекции равны 8 см и 36 см. Определите перпендикуляр.
чертеж пожалуйста ​

Answer 1

Ответ:

СН = 15 см

Пошаговое объяснение:

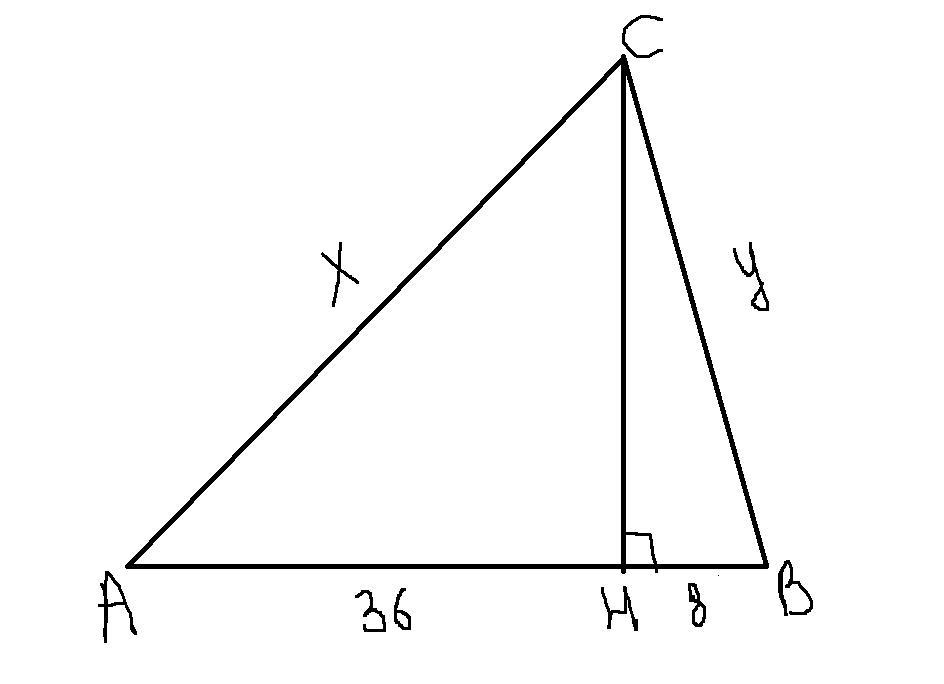
Дано: АВ - прямая

АС, ВС - наклонные

CH ⊥ АВ

AH = 36 см

BH = 8 см

AC+BC = 56 см

Найти: CH - ?

Решение: 1) Пусть AC=х, а BC=у, тогда

х+у = 56 ⇒ х = 56-у

2) Рассмотрим ΔАCH

ΔАCH - прямоугольный, т.к. CH ⊥ АВ

По т. Пифагора:

СН = √(АС²-АН²)

СН = √((56-у)²-36²)=√(3136-112у+у²-1296)=√(1840-112у+у²)

3) Рассмотрим ΔВCH

ΔВCH - прямоугольный, т.к. CH ⊥ АВ

По т. Пифагора:

СН = √(ВС²-ВН²)

СН = √(у²-8²)=√(у²-64)

4) Составим систему

$\displaystyle \left \{ {{CH=\sqrt{1840-112y+y^{2}} } \atop {CH=\sqrt{y^{2}-64} }} \right.$

Если равны левые части, то равны и правые

√(1840-112у+у²)=√(у²-64)

Возведём обе части

$\displaystyle \left \{ {\left\begin{array}{ccc}1840-112y+y^{2}=y^{2}-64\\1840-112y+y^{2} \geq 0\\y^{2}-64\geq 0\end{array}\right } \right.$

$\displaystyle \left \{ {\left\begin{array}{ccc}-112y=-64-1840|:(-112)\\(y-92)(y-20)\geq 0\\(y-8)(y+8)\geq 0\end{array}\right } \right.$

$\displaystyle \left \{ {\left\begin{array}{ccc}y=17\\\left[\begin{array}{ccc}y\leq 20\\y\geq 92\\\end{array}\right \\\left[\begin{array}{ccc}y\leq -8\\y\geq 8\\\end{array}\right\end{array}\right } \right.$

Значение y входит в заданное ОДЗ, вследствие чего можно сделать вывод, что ВС = 17 см

Теперь подставляю это значение в любое из выражений перпендикуляра

СН = √(17²-64)=√(289-64)=√225=15 см