Предмет: Алгебра,
автор: Аноним
решить матрицу методом крамера,без онлайн калькулятора
Приложения:
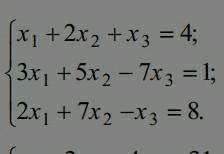
Ответы
Автор ответа:
0
Ответ:
(см. объяснение)
Объяснение:
Шаг 1:
Шаг 2:
Шаг 3:
Шаг 4:
Проверкой убеждаемся, что найденные числа удовлетворяют системе.
Задание выполнено!
Похожие вопросы
Предмет: Другие предметы,
автор: Паша1108
Предмет: Русский язык,
автор: Atartsa
Предмет: Українська мова,
автор: АринаДарьяСаша
Предмет: Математика,
автор: KristinaKristinag
Предмет: История,
автор: lazarevvlad2004