Предмет: Алгебра,
автор: Аноним
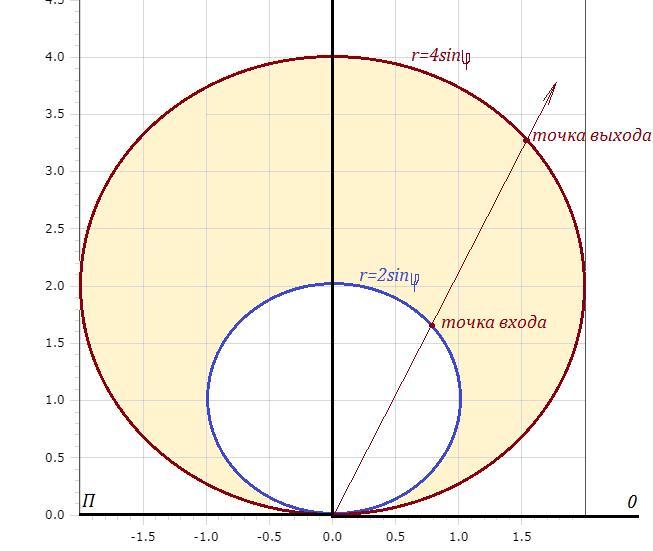
Вычислить площадь фигуры, ограниченной линиями.
Приложения:
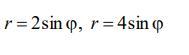
Ответы
Автор ответа:
1
Ответ:
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: Людмила1121
Предмет: Английский язык,
автор: Аноним
Предмет: Английский язык,
автор: terebonka2000
Предмет: Українська мова,
автор: TarasYakym1